期中微专题提分精炼2实数-2023-2024学年北师大版数学八年级上册

试卷更新日期：2023-10-28 类型：复习试卷

进入出卷网下载

一、选择题

1. 要使二次根式 $\sqrt{x - 2}$ 有意义，x的值可以是（）

A、3 B、1 C、0 D、-1

查看试题解析
2. 估计 $\sqrt{7}$ 的值应在（　　）

A、1到2之间 B、2到3之间 C、3到4之间 D、4到5之间

查看试题解析
3. 四个数0，1， $\sqrt{2}$ ， $\frac{1}{3}$ 中，无理数的是（）

A、 $\sqrt{2}$ B、1 C、 $\frac{1}{3}$ D、0

查看试题解析
4. 计算 $\sqrt{16}$ 的结果是（）

A、8 B、16 C、4 D、±4

查看试题解析
5. 下列运算结果正确的是（　　）

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt{(- 5)^{2}} = - 5$ C、 $(- \sqrt{2})^{2} = 2$ D、 $\sqrt{6} \div \sqrt{2} = 3$

查看试题解析
6. 下列各式中，最简二次根式是（　　）

A、 $\sqrt{0.2}$ B、 $\sqrt{18}$ C、 $\sqrt{x^{2} + 1}$ D、 $\sqrt{x^{2}}$

查看试题解析
7. 如图，表示 $- \sqrt{7}$ 的点落在（）

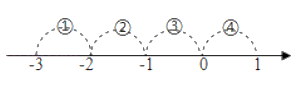A、段① B、段② C、段③ D、段④

查看试题解析
8. 如图，矩形 $A B C D$ 中， $A B = 3 ， A D = 1 ， A B$ 在数轴上，若以点A为圆心，对角线 $A C$ 的长为半径作到交数轴的正半轴于M，则点M，在数轴上表示的数为（）

A、2 B、 $\sqrt{5} - 1$ C、 $\sqrt{10} - 1$ D、 $\sqrt{5}$

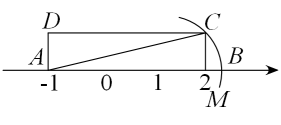查看试题解析
9. 下列计算正确的是（）

A、 $\sqrt[3]{- 8} = 2$ B、 $\sqrt{{(- 3)}^{2}} = - 3$ C、 $\sqrt{4} = 2$ D、 $\pm \sqrt{9} = 3$

查看试题解析
10. 下列各式运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{(- 4) \cdot (- 9)} = \sqrt{- 4} \cdot \sqrt{- 9} = (- 2) \cdot (- 3) = 6$ C、 $（ 2 \sqrt{10} - \sqrt{5} ） \div \sqrt{5} = 2 \sqrt{2} - 1$ D、 $\sqrt{5^{2} - 4^{2}} = \sqrt{5^{2}} - \sqrt{4^{2}} = 1$

查看试题解析

二、填空题

11. 已知m为正整数，若 $\sqrt{189 m}$ 是整数，则根据 $\sqrt{189 m} = \sqrt{3 \times 3 \times 3 \times 7 m} = 3 \sqrt{3 \times 7 m}$ 可知m有最小值 $3 \times 7 = 21$ ．设n为正整数，若 $\sqrt{\frac{200}{n}}$ 是大于1的整数，则n的最小值为．

查看试题解析
12. 若a，b是2022的两个平方根，则 $a + b - a b =$ .

查看试题解析
13. 已知 $R t △ A B C$ 的三边长为 $a$ ， $b$ ， $c$ ，且 $b$ 的两个平方根分别为 $2 a - 4$ 和 $1 - a$ ，则 $c$ 的值为．

查看试题解析
14. 如果 $\sqrt{2 x - 1}$ 有意义，那么x的取值范围是．

查看试题解析
15. 现定义一个新运算“※”，规定对于任意实数x，y，都有 $x ※ y = \sqrt{x + y} + \sqrt[3]{x y + 1}$ ，则 $7 ※ 9$ 的值为．

查看试题解析

三、计算题

16. 求下列各式中x的值．

(1)、 $x^{2} = \frac{9}{64}$ ；

(2)、 $2 {(x + 4)}^{3} + 128 = 0$ ；

查看试题解析
17. 计算： ${(\sqrt{6} - \sqrt{3})}^{2} - \sqrt{2} (\sqrt{8} - \sqrt{\frac{1}{2}})$ ．

查看试题解析
18. 计算：

(1)、 $\sqrt{12} - \sqrt{\frac{1}{3}} + \sqrt{3}$ ；

(2)、 $(\sqrt{5} + 1)^{2} - \sqrt{20}$ .

查看试题解析
19. 计算：

(1)、 $\frac{\sqrt{15} \times \sqrt{3}}{\sqrt{5}}$ ；

(2)、 $| 2 - \sqrt{5} | + \sqrt{\frac{1}{5}} \times \sqrt{20} - \sqrt{75}$ ．

查看试题解析
20. 计算：

(1)、 ${(π - 3)}^{0} - \sqrt{9} + \sqrt[3]{- 8} + | 1 - \sqrt{3} |$

(2)、 $\sqrt{48} \div \sqrt{2} - \sqrt{\frac{1}{2}} \times \sqrt{12} + 6 \sqrt{\frac{2}{3}}$

查看试题解析
21. 计算

(1)、 $2 \sqrt{\frac{1}{3}} \times \sqrt{9} - \sqrt{12} + \sqrt[3]{\frac{7}{8} - 1}$

(2)、 $\sqrt{8} - (2020 - π)^{0} + 2 | 1 - \sqrt{2} | + (- 3)^{2}$

查看试题解析

四、解答题

22. 化简并求值：已知 $x = \frac{2}{\sqrt{3} - 1}$ ，求 $x^{2} - 2 x + 3$ 的值．

查看试题解析
23. 已知正数a的两个平方根分别是 $2 x - 3$ 和 $1 - x$ ， $\sqrt[3]{1 - 2 b}$ 与 $\sqrt[3]{3 b - 5}$ 互为相反数．求 $a + 2 b$ 的算术平方根．

查看试题解析

五、综合题

24. 已知m是144的平方根，n是125的立方根．

(1)、求m、n的值；

(2)、求 $(m + 2 n)$ 的平方根．

查看试题解析
25. 我们知道， $（ \sqrt{3} ）^{2} = 3$ ， $(3 + \sqrt{5}) (3 - \sqrt{5}) = 3^{2} - {(\sqrt{5})}^{2} = 4$ ， …如果两个含有二次根式的非零代数式相乘，它们的积不含有二次根式，就说这两个非零代数式互为有理化因式.如 $3 + \sqrt{5}$ 与 $3 - \sqrt{5}$ 互为有理化因式.利用这种方法，可以将分母中含有二次根式的代数式化为分母是有理数的代数式，这个过程称为分母有理化，例如： $\frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{\sqrt{3}}{3}$ ， $\frac{1}{2 - \sqrt{3}} = \frac{2 + \sqrt{3}}{(2 - \sqrt{3}) (2 + \sqrt{3})} = \frac{2 + \sqrt{3}}{1} = 2 + \sqrt{3}$ .

(1)、 $\frac{2}{\sqrt{5}}$ 分母有理化的结果是；

(2)、 $\frac{1}{\sqrt{11} + \sqrt{10}}$ 分母有理化的结果是；

(3)、 $\frac{1}{\sqrt{n + 1} - \sqrt{n}}$ 分母有理化的结果是；

(4)、利用以上知识计算： $\frac{1}{1 + \sqrt{3}} + \frac{1}{\sqrt{3} + \sqrt{5}} + \frac{1}{\sqrt{5} + \sqrt{7}} + ⋯ + \frac{1}{\sqrt{2021} + \sqrt{2023}}$ .

查看试题解析