期中微专题提分精炼5一元二次方程-2023-2024学年北师大版九年级（上）数学

试卷更新日期：2023-10-28 类型：复习试卷

进入出卷网下载

一、选择题

1. 方程x² = 2x的解是（）.

A、 $x = 2$ B、 $x = 0$ C、 $x_{1} = 2$ ， $x_{2} = 0$ D、 $x_{1} = - 2$ ， $x_{2} = 0$

查看试题解析
2. 用配方法解方程 $x^{2} + 6 x + 4 = 0$ ，配方正确的是（）

A、 ${(x + 3)}^{2} = 5$ B、 ${(x + 3)}^{2} = 13$ C、 ${(x + 6)}^{2} = 5$ D、 ${(x + 6)}^{2} = 13$

查看试题解析
3. 用公式法解方程 $x^{2} - 2 x = 3$ 时，求根公式中的 $a$ ， $b$ ， $c$ 的值分别是（）

A、 $a = 1$ ， $b = - 2$ ， $c = 3$ B、 $a = 1$ ， $b = 2$ ， $c = - 3$ C、 $a = 1$ ， $b = 2$ ， $c = 3$ D、 $a = 1$ ， $b = - 2$ ， $c = - 3$

查看试题解析
4. 关于x的方程 $(a - 1) x^{2} + 3 x - 2 = 0$ 是一元二次方程的条件是（）

A、 $a \neq 0$ B、 $a = 1$ C、 $a \neq 1$ D、a为任意实数

查看试题解析
5. 一元二次方程 $2 (x^{2} - 1) - 3 x = 0$ 的二次项系数、一次项系数、常数项依次是（）

A、1，-1，-3 B、1，-3，-1 C、2，-3，-1 D、2，-3，-2

查看试题解析
6. 下列方程中，是一元二次方程的是（）

A、 $x^{2} - y^{2} - 3 = 0$ B、 $\frac{1}{5} x^{2} - x - 3 = 0$ C、 $a x^{2} - y - 3 = 0$ D、 $x^{2} - y - 3 = 0$

查看试题解析
7. 若一元二次方程 $5 x - 1 = 4 x^{2}$ 的两根为 $x_{1}$ 和 $x_{2}$ ，则 $x_{1} \cdot x_{2}$ 的值等于（）

A、1 B、 $\frac{1}{4}$ C、 $- \frac{1}{4}$ D、 $\frac{5}{4}$

查看试题解析
8. 新冠肺炎是一种传染性极强的疾病，如果有一人患病，经过两轮传染后有64人患病，设每轮传染中平均一个人传染了x个人，下列列式正确的是（）

A、 $x + x (1 + x) = 64$ B、 $1 + x + x^{2} = 64$ C、 $(1 + x)^{2} = 64$ D、 $x (1 + x) = 64$

查看试题解析
9. 已知关于x的一元二次方程 $(p + 1) x^{2} + 2 q x + (p + 1) = 0$ （其中p，q为常数）有两个相等的实数根，则下列结论中，错误的是（）．

A、1可能是方程 $x^{2} + q x + p = 0$ 的根 B、 $- 1$ 可能是方程 $x^{2} + q x + p = 0$ 的根 C、0可能是方程 $x^{2} + q x + p = 0$ 的根 D、1和 $- 1$ 都是方程 $x^{2} + q x + p = 0$ 的根

查看试题解析
10. 关于x的一元二次方程 $x^{2} + 2 m x + 2 n = 0$ 有两个整数根且乘积为正，关于y的一元二次方程 $y^{2} + 2 n y + 2 m = 0$ 同样也有两个整数根且乘积为正．给出四个结论：①这两个方程的根都是负根；② ${(m - 1)}^{2} + {(n - 1)}^{2} \geq 2$ ；③ $- 1 \leq 2 m - 2 n \leq 1$ ．其中正确结论的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

11. 某种植物的主干长出若干数目的枝干，每个枝干又长出同样数目的小分支，主干、支干和小分支的总数是91，那么每个支干长出小分支.

查看试题解析
12. 一元二次方程5x²– 3x = 4＋2x化为一般形式是．

查看试题解析
13. 如图所示，在一幅长 $50 c m$ 、宽 $30 c m$ 的风景画的四周镶一条金色纸边，制成一幅矩形挂图如图所示，如果要使整个矩形挂图的面积是 $3036 c m^{2}$ ，则金色纸边的宽为 cm.

查看试题解析
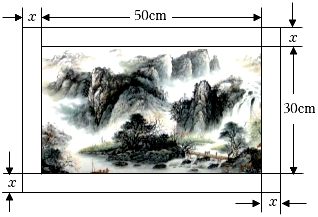14. 某厂家今年一月份的口罩产量是30万个，三月份的口罩产量是50万个，若设该厂家一月份到三月份的口罩产量的月平均增长率为x．则所列方程为

查看试题解析
15. 某种服装，平均每天可销售30件，每件赢利40元，网查发现，若每件降价1元，则每天可多售6件，如果每天要赢利2100元，每件应降价多少元？设该服装每件降价x元，根据题意可列方程．

查看试题解析

三、计算题

16. 解一元二次方程.

(1)、 $x^{2} - 4 x - 7 = 0$

(2)、 $(2 x + 1)^{2} - 4 (2 x + 1) = 0$

查看试题解析
17. 用指定的方法解下列方程．

(1)、用配方法解方程 $x^{2} - 10 x - 8 = 0$ ；

(2)、用公式法解方程 $3 x^{2} + 2 x = 4$ ．

查看试题解析
18. 解方程： $x^{2} - 6 x + 3 = 0$ ．

查看试题解析

四、解答题

19. 阅读下面的材料，并完成相应的任务．
材料：解含绝对值的方程： $x^{2} - 5 | x | - 6 = 0$ ．

解：分两种情况：

（ 1 ）当 $x \geq 0$ 时，原方程可化为： $x^{2} - 5 x - 6 = 0$ ，解得 $x_{1} = 6$ ， $x_{2} = - 1$ （舍去）；

（ 2 ）当 $x < 0$ 时，原方程可化为： $x^{2} + 5 x - 6 = 0$ ，解得 $x_{1} = - 6$ ， $x_{2} = 1$ （舍去）．

综上所述：原方程的解是 $x_{1} = 6$ ， $x_{2} = - 6$ ．任务：请参照上述方法解方程： $x^{2} - | x | - 2 = 0$ ．

查看试题解析
20. 解读诗词(通过列方程算出周瑜去世时的年龄)：大江东去浪淘尽，千古风流数人物，而立之年督东吴，早逝英年两位数，十位恰小个位三，个位平方与寿符，哪位学子算得快，多少年华属周瑜？诗词大意：周瑜三十岁当东吴都督，去世时的年龄是两位数，十位数字比个位数字小三，个位数字的平方等于他去世时的年龄.

查看试题解析

21. 小敏与小霞两位同学解方程

3 (x - 3) = {(x - 3)}^{2}

的过程如下框：

小敏：

两边同除以 $(x - 3)$ ，得

$3 = x - 3$ ，

则 $x = 6$ ．

小霞：

移项，得 $3 (x - 3) - {(x - 3)}^{2} = 0$ ，

提取公因式，得 $(x - 3) (3 - x - 3) = 0$ ．

则 $x - 3 = 0$ 或 $3 - x - 3 = 0$ ，

解得 $x_{1} = 3$ ， $x_{2} = 0$ ．

你认为他们的解法是否正确？若正确请在框内打“√”；若不正确请在框内打“×”，并写出你的解答过程．

查看试题解析

22. 对于实数u、v，定义一种运算“*”为： $u * v = u v + v$ ．若关于x的方程 $x * (a * x) = - \frac{1}{4}$ 有两个相等的实数根，求满足条件的实数a的值．

查看试题解析

五、综合题

23. 如图，用一段77米的篱笆围成三个一边靠墙、大小相同的矩形羊圈，每个矩形都有一个1米的门，墙的最大可用长度为30米．

(1)、如果羊圈的总面积为300平方米，求边 $A B$ 的长；

(2)、羊圈的总面积能为500平方米吗？若能，请求出边 $A B$ 的长；若不能，说明理由．

查看试题解析
24. 已知关于x的方程 $(k - 2) x^{2} - 2 x + 1 = 0$ 有两个实数根．

(1)、求k的取值范围；

(2)、当k取最大整数时，求此时方程的根．

查看试题解析
25. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ， $B C = a$ ， $A C = b (a < b)$ ， $A B = 5$ ， $a$ ， $b$ 是方程 $x^{2} - (m - 1) x + (m + 4) = 0$ 的两根.

(1)、求 $a$ ， $b$ ；

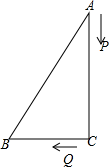(2)、 $P$ ， $Q$ 两点分别从 $A$ ， $C$ 出发，分别以每秒2个单位，1个单位的速度沿边 $A C$ ， $B C$ 向终点 $C$ ， $B$ 运动，（有一个点达到终点则停止运动），求经过多长时间后 $P Q = 2$ ？

查看试题解析
26. 对于任意一个三位数k，如果k满足各个数位上的数字都不为零，且十位上的数字的平方等于百位上的数字与个位上的数字之积的4倍，那么称这个数为“喜鹊数”．例如： $k = 169$ ，因为 $6^{2} = 4 \times 1 \times 9$ ，所以169是“喜鹊数”．

(1)、已知一个“喜鹊数” $k = 100 a + 10 b + c$ （ $1 \leq a 、 b 、 c \leq 9$ ，其中a，b，c为正整数），请直接写出a，b，c所满足的关系式；判断241 “喜鹊数”（填“是”或“不是”）；

(2)、利用（1）中“喜鹊数”k中的a，b，c构造两个一元二次方程 $a x^{2} + b x + c = 0$ ①与 $c x^{2} + b x + a = 0$ ②，若 $x = m$ 是方程①的一个根， $x = n$ 是方程②的一个根，求m与n满足的关系式；

(3)、在（2）中条件下，且 $m + n = - 2$ ，请直接写出满足条件的所有k的值．

查看试题解析