江苏省南京市六校联考2023-2024学年高三上册数学月考试卷
试卷更新日期:2023-10-27 类型:月考试卷
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 若复数满足 , 则等于( )A、 B、 C、 D、2. 已知集合 , , ( )A、 B、 C、 D、3. 等差数列的前项和为 , 且 , , 则( )A、 B、 C、 D、4. 从位男生,位女生中安排人到三个场馆做志愿者,每个场馆各人,且至少有位男生入选,则不同安排方法有种( )A、 B、 C、 D、5. “”是“直线与圆相切”的条件.( )A、充分不必要 B、必要不充分 C、充要 D、既不充分也不必要6. 在平面直角坐标系中,双曲线:的左、右焦点分别为 , , 过且垂直于轴的直线与交于 , 两点,与轴的交点为 , , 则的离心率为( )A、 B、 C、 D、7. 已知 , 则( )A、 B、 C、 D、8. 已知函数及其导函数的定义域均为 , 记 , 若 , 均为偶函数,则下列等式一定正确的是( )A、 B、 C、 D、
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
-
9. 给出下列命题中,其中正确的命题是( )A、随机变量 , 则 B、已知 , , 则 C、随机变量 , 若 , 则 , D、以模型拟合一组数据时,为了求回归方程,设 , 将其变换后得到线性方程 , 则 , 的值分别是和10. 已知函数的图象如图所示,则( )
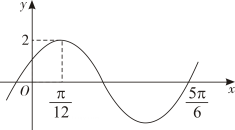 A、函数解析式 B、将函数的图象向左平移个单位长度可得函数的图象 C、直线是函数图象的一条对称轴 D、函数在区间上的最大值为11. 如果有限数列满足 , 则称其为“对称数列”,设是项数为的“对称数列”,其中 , , , 是首项为 , 公差为的等差数列,则( )A、若 , 则 B、若 , 则所有项的和为 C、当时,所有项的和最大 D、所有项的和可能为12. 如图,在菱形中, , , 为的中点,将沿直线翻折到的位置,连接和 , 为的中点,在翻折过程中,则下列结论中正确的是( )
A、函数解析式 B、将函数的图象向左平移个单位长度可得函数的图象 C、直线是函数图象的一条对称轴 D、函数在区间上的最大值为11. 如果有限数列满足 , 则称其为“对称数列”,设是项数为的“对称数列”,其中 , , , 是首项为 , 公差为的等差数列,则( )A、若 , 则 B、若 , 则所有项的和为 C、当时,所有项的和最大 D、所有项的和可能为12. 如图,在菱形中, , , 为的中点,将沿直线翻折到的位置,连接和 , 为的中点,在翻折过程中,则下列结论中正确的是( ) A、面面 B、线段长度的取值范围为 C、直线和所成的角始终为 D、当三棱锥的体积最大时,点在三棱锥外接球的外部
A、面面 B、线段长度的取值范围为 C、直线和所成的角始终为 D、当三棱锥的体积最大时,点在三棱锥外接球的外部三、填空题(本大题共4小题,共20.0分)
-
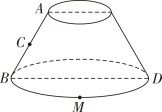
13. 的展开式的中间项的系数是用数字作答 .14. 已知向量 , , 则向量在向量上的投影向量的坐标为 .15. 函数为在定义域内为增函数,则实数的取值范围为 .16. 如图是圆台母线的中点,是底面的直径,上底面半径为 , 下底面半径为 , , 点是弧的中点,则、两点在圆台侧面上连线长最小值的平方等于 .
四、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
-
17. 已知数列的前项和为 , 且 , .(1)、求的通项公式;(2)、若 , , 求 .18. 请从下面三个条件中任选一个,补充在下面的横线上,并解答.
;
;
.
在中,内角 , , 的对边分别是 , , , 若.
(1)、求角;(2)、若 , 求周长的取值范围.19. 已知四棱锥中,平面 , , , , . (1)、求证:平面平面;(2)、设是棱上的点,若二面角的余弦值为 , 试求直线与平面所成角的正弦值.20. 已知椭圆:的左、右顶点分别 , , 上顶点为 , , 的长轴长比短轴长大 .(1)、求椭圆的方程;(2)、斜率存在且不为的直线交椭圆于 , 两点异于点 , 且 , 证明:直线恒过定点,并求出定点坐标.21. 2019年春节期间,我国高速公路继续执行“节假日高速公路免费政策”某路桥公司为掌握春节期间车辆出行的高峰情况,在某高速公路收费站点记录了大年初三上午::这一时间段内通过的车辆数,统计发现这一时间段内共有辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如下图所示,其中时间段::记作区 , ::记作 , ::记作 , ::记作 , 例如点分,记作时刻 .
(1)、求证:平面平面;(2)、设是棱上的点,若二面角的余弦值为 , 试求直线与平面所成角的正弦值.20. 已知椭圆:的左、右顶点分别 , , 上顶点为 , , 的长轴长比短轴长大 .(1)、求椭圆的方程;(2)、斜率存在且不为的直线交椭圆于 , 两点异于点 , 且 , 证明:直线恒过定点,并求出定点坐标.21. 2019年春节期间,我国高速公路继续执行“节假日高速公路免费政策”某路桥公司为掌握春节期间车辆出行的高峰情况,在某高速公路收费站点记录了大年初三上午::这一时间段内通过的车辆数,统计发现这一时间段内共有辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如下图所示,其中时间段::记作区 , ::记作 , ::记作 , ::记作 , 例如点分,记作时刻 .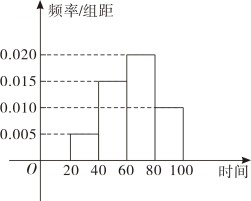 (1)、估计这辆车在::时间内通过该收费点的时刻的平均值同一组中的数据用该组区间的中点值代表;(2)、为了对数据进行分析,现采用分层抽样的方法从这辆车中抽取辆,再从这辆车随机抽取辆,设抽到的辆车中,在::之间通过的车辆数为 , 求的分布列与数学期望;(3)、由大数据分析可知,车辆在每天通过该收费点的时刻服从正态分布 , 其中可用这辆车在::之间通过该收费点的时刻的平均值近似代替,可用样本的方差近似代替同一组中的数据用该组区间的中点值代表 , 已知大年初五全天共有辆车通过该收费点,估计在::之间通过的车辆数结果保留到整数 .
(1)、估计这辆车在::时间内通过该收费点的时刻的平均值同一组中的数据用该组区间的中点值代表;(2)、为了对数据进行分析,现采用分层抽样的方法从这辆车中抽取辆,再从这辆车随机抽取辆,设抽到的辆车中,在::之间通过的车辆数为 , 求的分布列与数学期望;(3)、由大数据分析可知,车辆在每天通过该收费点的时刻服从正态分布 , 其中可用这辆车在::之间通过该收费点的时刻的平均值近似代替,可用样本的方差近似代替同一组中的数据用该组区间的中点值代表 , 已知大年初五全天共有辆车通过该收费点,估计在::之间通过的车辆数结果保留到整数 .若则 , , .
22. 已知函数 , , , .(1)、当时,求函数的单调区间.(2)、若曲线在点处的切线与曲线切于点 , 求 , , 的值.(3)、若恒成立,求的最大值.