江苏省苏州市常熟市2023-2024学年高二上册数学暑期调查试卷

试卷更新日期：2023-10-27 类型：开学考试

进入出卷网下载

一、单选题（本大题共8小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）

1. 已知集合 $S = {s | s = 2 n + 1 ， n \in Z}$ ， $T = {t | t = 4 n + 1 ， n \in Z}$ ，则 $S \cap^{} T =$ （）

A、 $\emptyset$ B、 $S$ C、 $T$ D、 $Z$

查看试题解析
2. 已知命题 $p$ ： $\forall x < 0$ ， $x^{2} > 0$ ，则 $p$ 的否定是（）

A、 $\forall x < 0$ ， $x^{2} < 0$ B、 $\forall x < 0$ ， $x^{2} \leq 0$ C、 $\exists x < 0$ ， $x^{2} < 0$ D、 $\exists x < 0$ ， $x^{2} \leq 0$

查看试题解析
3. 在空间中， $l$ ， $m$ 是不重合的直线， $α$ ， $β$ 是不重合的平面，则下列说法正确的是（）

A、若 $l \subset α$ ， $m \subset β$ ， $α / / β$ ，则 $l / / m$ B、若 $l / / m$ ， $m \subset β$ ，则 $l / / β$ C、若 $α ⊥ β$ ， $α \cap^{} β = m$ ， $l ⊥ m$ ，则 $l ⊥ β$ D、若 $l ⊥ α$ ， $l / / m$ ， $α / / β$ ，则 $m ⊥ β$

查看试题解析
4. 函数 $y = (2^{x} - 2^{- x}) \sin x$ 在 $[- π ， π]$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
5. 如图，在平行四边形 $A B C D$ 中， $A E = \frac{1}{3} A B ， C F = \frac{1}{3} C D ， G$ 为 $E F$ 的中点，则 $\vec{D G} =$ （）

A、 $\frac{1}{2} \vec{A B} - \frac{1}{2} \vec{A D}$ B、 $\frac{1}{2} \vec{A D} - \frac{1}{2} \vec{A B}$ C、 $\frac{1}{3} \vec{A B} - \frac{1}{3} \vec{A D}$ D、 $\frac{1}{3} \vec{A D} - \frac{1}{3} \vec{A B}$

查看试题解析
6. 已知 $s i n (α + \frac{π}{3}) = \frac{3}{5}$ ， $α \in (- \frac{π}{2} ， \frac{π}{6})$ ，则 $s i n α$ 的值为（）

A、 $\frac{3 - 4 \sqrt{3}}{10}$ B、 $\frac{3 + 4 \sqrt{3}}{10}$ C、 $\frac{3 - 2 \sqrt{3}}{10}$ D、 $\frac{3 + 2 \sqrt{3}}{10}$

查看试题解析
7. 古代数学家刘徽编撰的 $《$ 重差 $》$ 是中国最早的一部测量学著作，也为地图学提供了数学基础 $.$ 现根据刘徽的 $《$ 重差 $》$ 测量一个球体建筑物的高度，已知点 $A$ 是球体建筑物与水平地面的接触点 $($ 切点 $)$ ，地面上 $B$ ， $C$ 两点与点 $A$ 在同一条直线上，且在点 $A$ 的同侧 $.$ 若在 $B$ ， $C$ 处分别测得球体建筑物的最大仰角为 $60 °$ 和 $20 °$ ，且 $B C = 100 m$ ，则该球体建筑物的高度约为（）

A、 $\frac{25}{c o s 1 0^{∘}} m$ B、 $\frac{50}{c o s 1 0^{∘}} m$ C、 $\frac{25}{s i n 1 0^{∘}} m$ D、 $\frac{50}{s i n 1 0^{∘}} m$

查看试题解析
8. 在四面体 $A B C D$ 中，已知二面角 $A - B D - C$ 为直二面角， $∠ B A D = 90 °$ ， $∠ C B D = 45 °$ ， $A B = A D = \sqrt{3}$ ，设 $A C = t (t > 0) .$ 若满足条件的四面体 $A B C D$ 有两个，则 $t$ 的取值范围是（）

A、 $(0 ， \sqrt{3})$ B、 $(0 ， \frac{3}{2})$ C、 $(\sqrt{3} ， 3)$ D、 $(\frac{3}{2} ， \sqrt{3})$

查看试题解析

二、多选题（本大题共4小题，共20.0分。在每小题有多项符合题目要求）

9. 已知 $i$ 为虚数单位，以下四个说法中正确的是（）

A、 $i + i^{2} + i^{3} + i^{4} = 0$ B、 $3 + i > 1 - i$ C、若 $z = (1 + 2 i)^{2}$ ，则复数 $z$ 对应的点位于第四象限 D、已知复数 $z$ 满足： $| z - 2 i | = 3$ ，则 $z$ 在复平面内对应的点的轨迹为圆

查看试题解析
10. 袋子中有5个大小质地完全相同的球，分别标有数字1，2，3，4，5，从中有放回地依次随机摸出2个球，甲表示事件“第一次取出的球的数字是1”，乙表示事件“第一次取出的球的数字是偶数”，丙表示事件“两次取出的球的数字都是偶数”，丁表示事件“两次取出的球的数字之和为6”，则（）

A、甲与乙是对立事件 B、甲与乙是互斥事件 C、丙与丁相互独立 D、甲与丁相互独立

查看试题解析
11. 若定义在 $R$ 上的奇函数 $f (x)$ 满足 $f (x) = f (2 - x)$ ，且当 $x \in (0 ， 1]$ 时， $f (x) = x$ ，则（）

A、 $y = f (x + 1)$ 为偶函数 B、 $f (x)$ 在 $(3 ， 5)$ 上单调递增 C、 $f (x)$ 在 $(- 3 ， - 1)$ 上单调递增 D、 $f (x)$ 的最小正周期 $T = 4$

查看试题解析
12. 如图，若正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为 $2$ ，点 $M$ 是正方体在侧面 $B C C_{1} B_{1}$ 上的一个动点 $($ 含边界 $)$ ，点 $P$ 是 $A A_{1}$ 的中点，则下列结论正确的是（）

A、三棱锥 $P - D D_{1} M$ 的体积为定值 B、四棱锥 $P - B D D_{1} B_{1}$ 外接球的半径为 $\frac{5 \sqrt{2}}{4}$ C、若 $D_{1} M ⊥ D P$ ，则 $A_{1} M$ 的最大值为 $2 \sqrt{2}$ D、若 $D_{1} M ⊥ D P$ ，则 $A_{1} M$ 的最小值为 $\frac{6 \sqrt{5}}{5}$

查看试题解析

三、填空题（本大题共4小题，共20.0分）

13. 计算： $l o g_{3} 12 + 2^{1 + l o g_{2} 5} - l o g_{3} 4 =$ ．

查看试题解析
14. 若圆锥侧面展开图是圆心角为 $\frac{2 π}{3}$ ，半径为 $2$ 的扇形，则这个圆锥表面积为．

查看试题解析
15. 请写出一个定义域不是 $R$ ，但值域为 $R$ 的奇函数： $f (x) =$ ．

查看试题解析
16. 在锐角三角形ABC中，已知 $2 s i n^{2} A + s i n^{2} B = 2 s i n^{2} C$ ，则 $\frac{t a n C}{t a n A} =$ ， $\frac{1}{t a n A} + \frac{1}{t a n B} + \frac{1}{t a n C}$ 的最小值是.

查看试题解析

四、解答题（本大题共6小题，共70.0分。解答应写出文字说明，证明过程或演算步骤）

17. 已知复数 $z = (m - 1) + (m + 1) i (m \in R)$ ．

(1)、若 $z$ 在复平面内的对应点位于第二象限，求 $m$ 的取值范围；

(2)、若 $z$ 为纯虚数，设 $z^{3}$ ， $z^{2} - z$ 在复平面上对应的点分别为 $A$ ， $B$ ，求向量 $\vec{O A}$ 在向量 $\vec{O B}$ 上的投影向量的坐标．

查看试题解析
18. 某企业为了深入学习贯彻党的二十大精神，组织全体 $120$ 位党员开展“学习二十大，争当领学人”党史知识竞赛，所有党员的成绩均在 $[75 ， 100]$ 内，成绩分成 $5$ 组，按照下面分组进行统计分析：第 $1$ 组 $[75 ， 80)$ ，第 $2$ 组 $[80 ， 85)$ ，第 $3$ 组 $[85 ， 90)$ ，第 $4$ 组 $[90 ， 95)$ ，第 $5$ 组 $[95 ， 100]$ ，并绘制成频率分布直方图如图所示，按比例分配的分层抽样的方法在第 $3$ ， $4$ ， $5$ 组共选取 $6$ 人作为企业“二十大精神”的宣传使者．

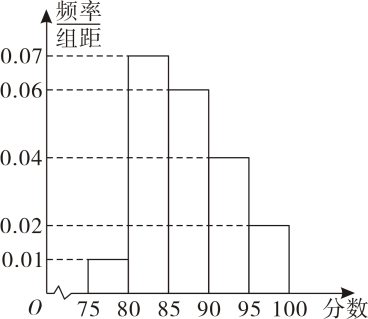(1)、根据频率分布直方图，估计党员成绩的样本数据的第 $80$ 百分位数；

(2)、若从 $6$ 位宣传使者中随机选取两人参加宣传活动，求第 $3$ 组中至多有一人被选中的概率．

查看试题解析
19. 已知函数 $f (x) = \sqrt{3} s i n (ω x + φ) + 1 - 2 c o s^{2} (\frac{ω x + φ}{2}) (ω > 0 ， 0 < φ < π)$ 为奇函数，且 $f (x)$ 图象的相邻两对称轴间的距离为 $\frac{π}{2}$ ．

(1)、求 $f (x)$ 的解析式及单调减区间；

(2)、将函数 $f (x)$ 的图象向右平移 $\frac{π}{6}$ 个单位长度，再把横坐标缩小为原来的 $\frac{1}{2} ($ 纵坐标不变 $)$ ，得到函数 $y = g (x)$ 的图象，当 $x \in [- \frac{π}{8} ， \frac{π}{2}]$ 时，求方程 $g^{2} (x) + 3 \sqrt{3} \cdot g (x) + 6 = 0$ 的所有根之和．

查看试题解析
20. 记 $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 的对边分别为 $a$ ， $b$ ， $c$ ，已知 $△ A B C$ 面积为 $\sqrt{3}$ ， $D$ 为 $B C$ 的中点，且 $A D = 1$ ．

(1)、若 $∠ A D C = \frac{π}{3}$ ，求 $t a n B$ ；

(2)、若 $b^{2} + c^{2} = 8$ ，求 $b$ ， $c$ ．

查看试题解析
21. 如图，在四棱锥 $P - A B C D$ 中， $P A ⊥$ 平面 $A B C D$ ， $A D / / B C$ ， $A D ⊥ C D$ ，且 $A D = C D = 2$ ， $B C = 4$ ， $P A = \sqrt{2}$ ．

(1)、求证： $A B ⊥ P C$ ；

(2)、已知 $M$ 为线段 $P D$ 上一点，若 $B M$ 与平面 $A B C D$ 所成角的正切值为 $\frac{\sqrt{26}}{26}$ ，试确定 $M$ 点位置；并求此时二面角 $M - A C - D$ 的大小．

查看试题解析
22. 已知函数 $y = a^{x - 1} - 1 (a > 0 ， a \neq 1)$ 过定点 $A$ ，且点 $A$ 在函数 $f (x) = l n (x + t) (t \in R)$ 的图象上， $g (x) = x^{2} - 2 e^{f (x)}$ ．

(1)、求函数 $f (x)$ 的解析式；

(2)、若定义在区间 $(1 ， 2)$ 上的函数 $y = f (x) + l n (2 x - k)$ 有零点，求整数 $k$ 的值；

(3)、设 $m > 0$ ，若对于任意 $x \in [\frac{1}{m} ， m]$ ，都有 $g (x) < - l n (m - 1)$ ，求 $m$ 的取值范围．

查看试题解析