北师大版数学七年级(上)复习微专题精炼12 探索与表达规律
试卷更新日期:2023-10-26 类型:复习试卷
一、选择题
-
1. 观察下列算式:;;;;;……,则的末尾数字是( )A、1 B、5 C、7 D、92. 找出以如图形变化的规律,则第2021个图形中黑色正方形的数量是( )
 A、3030 B、3032 C、2020 D、20213. ( )A、-1011 B、1011 C、-1012 D、10124. 观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…用你所发现的规律得出22022的末位数字是( ).A、2 B、4 C、6 D、85. 用形状相同的两种菱形拼成如图所示的图案,用an表示第n个菱形的个数,则an(用含n的式子表示)为( )
A、3030 B、3032 C、2020 D、20213. ( )A、-1011 B、1011 C、-1012 D、10124. 观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…用你所发现的规律得出22022的末位数字是( ).A、2 B、4 C、6 D、85. 用形状相同的两种菱形拼成如图所示的图案,用an表示第n个菱形的个数,则an(用含n的式子表示)为( ) A、5n-1 B、8n-4 C、6n-2 D、4n+46. 一杯饮料,第1次倒去 , 第2次倒去剩下的 , 如此倒下去,倒5次后剩下的饮料是原来的( )A、 B、 C、 D、7. 将正偶数按下表排成5列:
A、5n-1 B、8n-4 C、6n-2 D、4n+46. 一杯饮料,第1次倒去 , 第2次倒去剩下的 , 如此倒下去,倒5次后剩下的饮料是原来的( )A、 B、 C、 D、7. 将正偶数按下表排成5列:第1列
第2列
第3列
第4列
第5列
第1行
2
4
6
8
第2行
16
14
12
10
第3行
18
20
22
24
28
26
若2022在第m行第n列,则( )
A、256 B、257 C、510 D、5118. a是不为2的有理数,我们把称为a的“哈利数”,如3的“哈利数”是=-2,-2的“哈利数”是.已知a1=3,a2是a1的“哈利数”,a3是a2的“哈利数”,a4是a3的“哈利数”,……依此类推,则a2023=( )A、3 B、-2 C、 D、9. 下列哪一幅图的规律和其他图不一样?( )A、 B、
B、 C、
C、 D、
D、 10. 将一列有理数 , ……,如图所示有序排列.根据图中的排列规律可知,“峰1”中峰顶的位置(的位置)是有理数4,那么,“峰6”中的位置是有理数____,2022应排在、、、、中____的位置.正确的选项是( )
10. 将一列有理数 , ……,如图所示有序排列.根据图中的排列规律可知,“峰1”中峰顶的位置(的位置)是有理数4,那么,“峰6”中的位置是有理数____,2022应排在、、、、中____的位置.正确的选项是( )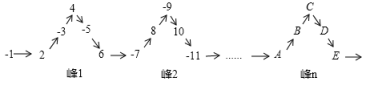 A、-29, B、30, C、029, D、-31,
A、-29, B、30, C、029, D、-31,二、填空题
-
11. 古希腊数学家把数1,3,6,10,15,21,…叫做三角数,它有一定的规律性.若把第一个三角数记为 , 第二个三角数记为 , …,第n个三角数记为 , 则().12. 有依次排列的3个数:2,6,7,对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:2,4,6,1,7,这称为第一次操作;做第二次同样的操作后也产生一个新数串:2,2,4,2,6, , 1,6,7,若相继依次操作,则从数串:2,6,7开始操作第100次时所产生的那个新数串的所有数之和是 .13. 如图所示的三角形数阵叫“莱布尼茨调和三角形”,它们是由整数的倒数组成的,第n行有n个数,且两端的数均为 , 每个数是它下一行左右相邻两数的和,则第8行第3个数(从左往右数)为;
……
14. 观察下列一组数的规律,填上合适的数 .15. 已知整数 , , , , …满足下列条件: , , , , 以此类推,则的值为.三、计算题
-
16. 计算:(1)、1+2﹣3﹣4+5+6﹣7﹣8+…+2017+2018﹣2019﹣2020+2021;(2)、(﹣1)+(﹣2021)﹣(﹣4040)+(﹣1013)+(﹣1005).17. 观察下列算式:
;①
;②
;③
………按照上面的规律完成下列各题:
(1)、第④个算式:;(2)、第⑤个算式为;(3)、第 n 个算式为;(4)、计算:.四、解答题
-
18. 如表所示的数中,第个数比第个数大2(其中是正整数).
第1个数
第2个数
第3个数
第4个数
第5个数
…
…
(1)、第个数可表示为;第个数可表示为;(2)、第个数是 , 第个数为 , 则 , ;(3)、第个数可表示为 .19. 如图①②③是将正方体截去一部分后得到的几何体. (1)、根据要求填写表格:
(1)、根据要求填写表格:图
面数(f)
顶点数(v)
棱数(e)
①
②
③
(2)、猜想f,v,e三个数量间有何关系;(3)、根据猜想计算,若一个几何体有2021个顶点,4035条棱,试求出它的面数.20. 利用图形来表示数量或数量关系,也可以利用数量或数量关系来描述图形特征或图形之间的关系,这种思想方法称为数形结合.请你尝试利用数形结合的思想方法解决下列问题 (1)、如图①,一个边长为1的正方形,依次取正方形面积的 , 根据图示我们可以知道:= . (用含有n的式子表示)(2)、如图②,一个边长为1的正方形,第一次取正方形面积的 , 然后依次取剩余部分的 , 根据图示:计算:= . (用含有n的式子表示)(3)、如图③是一个边长为1的正方形,根据图示:计算:= . (用含有n的式子表示)21. 我校七年级数学兴趣小组成员们自主开展数学微项目研究.结合本阶段学内容特点,他们决定研究数的一些“神秘”性质.
(1)、如图①,一个边长为1的正方形,依次取正方形面积的 , 根据图示我们可以知道:= . (用含有n的式子表示)(2)、如图②,一个边长为1的正方形,第一次取正方形面积的 , 然后依次取剩余部分的 , 根据图示:计算:= . (用含有n的式子表示)(3)、如图③是一个边长为1的正方形,根据图示:计算:= . (用含有n的式子表示)21. 我校七年级数学兴趣小组成员们自主开展数学微项目研究.结合本阶段学内容特点,他们决定研究数的一些“神秘”性质.探索数的神秘性质
素材
尼科马霍斯是古希腊数学家,他的著作算术入门中记载了各种数分门别类的整理成果,其中任何一个整数的立方都可以写成个连续奇数之和.
举例论证:
;;;
请你按规律写出:
▲ .
规律总结
当是奇数7时,则等号右边式子中的中间数即第4个数为 ▲ ;
当为偶数10时,则等号右边式子中的中间两个数即第5和第6个数为 ▲ .
综合应用
利用上面结论计算:.
拓展延伸
我们还发现以下规律:已知 , , 且 , 均为正整数,如果将进行如图所示的“分解”:
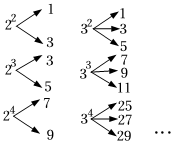
若且 , 均为不大于的正整数的分解中有奇数31,则的值为 ▲ .