北师版数学七年级上册单元清测试（第三章）培优卷

试卷更新日期：2023-10-26 类型：单元试卷

进入出卷网下载

一、选择题

1. 下列计算正确的是（　　）

A、 $4 a - 2 a = 2$ B、 $2 a b + 3 b a = 5 a b$ C、 $a + a^{2} = a^{3}$ D、 $5 x^{2} y - 3 x y^{2} = 2 x y$

查看试题解析
2. 我们知道，用字母表示的代数式是具有一般意义的，请仔细分析下列赋予3a实际意义的例子中不正确的是（）

A、若葡萄的价格是3元/千克，则3a表示买a千克葡萄的金额 B、若a表示一个等边三角形的边长，则3a表示这个等边三角形的周长 C、将一个小木块放在水平桌面上，若3表示小木块与桌面的接触面积，a表示桌面受到的压强，则3a表示小木块对桌面的压力 D、若3和a分别表示一个两位数中的十位数字和个位数字，则3a表示这个两位数

查看试题解析
3. 将x克含糖10%的糖水与y克含糖30%的糖水混合，混合后的糖水含糖（）

A、20% B、 $\frac{x + y}{2}$ ×100% C、 $\frac{x + 3 y}{20}$ ×100% D、 $\frac{x + 3 y}{10 x + 10 y}$ ×100%

查看试题解析
4. 若 $m^{2} + 2 m - 1 = 0$ ．则 $2 m^{2} + 4 m - 3$ 的值是（）

A、 $- 1$ B、 $- 5$ C、5 D、 $- 3$

查看试题解析
5. 我国南宋时期数学家杨辉于 $1261$ 年写下的 $《$ 详解九章算法 $》$ ，书中记载的图表给出了 $(a + b)^{n}$ 展开式的系数规律．

当代数式 $x^{4} - 12 x^{3} + 54 x^{2} - 108 x + 81$ 的值为 $1$ 时，则 $x$ 的值为（）

A、 $2$ B、 $- 4$ C、 $2$ 或 $4$ D、 $2$ 或 $- 4$

查看试题解析
6. 单项式x^m^﹣¹y³与4xyⁿ的和是单项式，则n^m的值是（）

A、3 B、6 C、8 D、9

查看试题解析
7. 已知一列均不为1的数 $a_{1} ， a_{2} ， a_{3} ， ⋯ ， a_{n}$ 满足如下关系： $a_{2} = \frac{1 + a_{1}}{1 - a_{1}} ， a_{3} = \frac{1 + a_{2}}{1 - a_{2}}$ ， $a_{4} = \frac{1 + a_{3}}{1 - a_{3}} ， ⋯ ， a_{n + 1} = \frac{1 + a_{n}}{1 - a_{n}}$ ，若 $a_{1} = 2$ ，则 $a_{2023}$ 的值是（）

A、 $- \frac{1}{2}$ B、 $\frac{1}{3}$ C、 $- 3$ D、2

查看试题解析

8. 在日历上，某些数满足一定的规律．如图是某年8月份的日历，任意选择其中所示的含4个数字的方框部分，设右上角的数字为a，则下列叙述中正确的是（）．

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

A、左上角的数字为

a + 1

B、左下角的数字为

a + 7

C、右下角的数字为

a + 8

D、方框中4个位置的数相加，结果是4的倍数

查看试题解析

9. 如图，输入数值1921，按所示的程序运算（完成一个方框内的运算后，把结果输入下一个方框继续进行运算），输出的结果为（）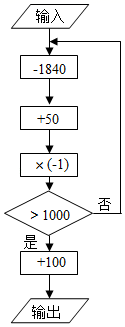

A、1840 B、1921 C、1949 D、2021

查看试题解析
10. 如图，用相同的圆点按照一定的规律拼出图形．第一幅图4个圆点，第二幅图7个圆点，第三幅图10个圆点，第四幅图13个圆点……按照此规律，第一百幅图中圆点的个数是（）

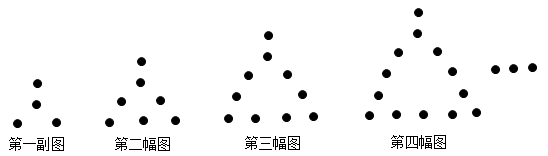A、297 B、301 C、303 D、400

查看试题解析

二、填空题

11. 若多项式 $x y^{| m - n |} + (n - 2) x^{2} y^{2} + 1$ 是关于x，y的三次多项式，则 $m n =$ ．

查看试题解析
12. 当 $a + b = 3$ 时，代数式 $2 (a + 2 b) - (3 a + 5 b) + 5$ 的值为．

查看试题解析
13. 计算： $3 a^{2} - 2 a^{2} =$ ．

查看试题解析
14. 若 $7 x^{m} y^{3}$ 和 $\frac{1}{2} y^{n} x^{2}$ 是同类项，则 $m - n =$ ．

查看试题解析
15. 在求 $1 + 2 + 3 + ⋯ ⋯ + 100$ 的值时，发现： $1 + 100 = 101$ ， $2 + 99 = 101 ⋯ ⋯$ ，从而得到 $1 + 2 + 3 + ⋯ + 100 =$ $101 \times 50 = 5050$ .按此方法可解决下面问题.图（1）有1个三角形，记作 $a_{1} = 1$ ；分别连接这个三角形三边中点得到图（2），有5个三角形，记作 $a_{2} = 5$ ；再分别连接图（2）中间的小三角形三边中点得到图（3），有9个三角形，记作 $a_{3} = 9$ ；按此方法继续下去，则 $a_{1} + a_{2} + a_{3} + ⋯ ⋯ + a_{n} =$ .（结果用含n的代数式表示）

查看试题解析
16. a是不为1的有理数，我们把 $\frac{1}{1 - a}$ 称为a的差倒数．如：2的差倒数是 $\frac{1}{1 - 2}$ ＝-1，-1的差倒数 $\frac{1}{1 - (- 1)} = \frac{1}{2}$ ，已知a₁＝- $\frac{1}{3}$ ， a₂是a₁的差倒数，a₃是a₂的差倒数，a₄是a₃的差倒数，…，依此类推，则a₂₀₂₀＝．

查看试题解析

三、解答题

17. 先化简，再求值： $5 (3 a^{2} b - a b^{2} + 1) - 4 (- a b^{2} + 3 a^{2} b - 1)$ ，其中 $a = \frac{1}{2}$ ， $b = - 4$

查看试题解析
18. 先化简，再求值： $3 a b - [2 a^{2} - (b^{2} - 3 a b) - a^{2}]$ ，其中 $a = - 2$ ， $b = 3$

查看试题解析
19. 先化简，再求值： $2 (a^{2} + a b) - [2 a^{2} - 3 b + 3 (a b + b)]$ ，其中 $a = 6$ ， $b = - \frac{1}{3}$ .

查看试题解析
20. 化简并求值： $2 (\frac{1}{2} x^{2} - 3 x y - y^{2}) - (x^{2} - 5 x y - 2 y^{2})$ ，其中 $x = 2 ， y = 1$ .

查看试题解析
21. 已知A=x²-3xy-y，B=-x²-xy+3y．

(1)、化简A-B．

(2)、当-ab^y⁺³与 $\frac{1}{2}$ a^x+3b²是同类项时，求A-B的值．

查看试题解析
22. 某展览馆周内仅上午开放可供游客观展，已知八点钟开馆时进入游客 $(a + 2 b)$ 人，中途陆陆续续有 $\frac{1}{3}$ 的游客离开，又进来若干游客，十一点时馆内共有游客 $(3 a + 3 b)$ 人.

(1)、从八点钟开馆到十一点这段时间内馆内一直不变的游客有人；（用含有a ， b的式子表示）

(2)、求中途进来的游客有多少人；（用含有a ， b的式子表示并化简）

(3)、当 $a = 3$ ， $b = 9$ 时，中途进来的游客有多少人？

查看试题解析
23. 用火柴棒按图中的方式搭图形．如图所示：
图形标号
①
②
③
④
⑤
…
火柴棒根数
5
9
13
17
$a$
…

(1)、根据规律填空： $a =$ ；

(2)、按照这种方式搭下去，搭第n个图形需要火柴棒的根数为；（含n的式了表示）

(3)、按这种方式搭下去，用（2）中的式子求第多少个图形需要4045根火柴？

查看试题解析

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

图形标号	①	②	③	④	⑤	…
火柴棒根数	5	9	13	17	$a$	…

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

北师版数学七年级上册单元清测试（第三章） 培优卷

一、选择题

二、填空题

三、解答题

北师版数学七年级上册单元清测试（第三章）培优卷

日	一	二	三	四	五	六
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31