北师大版数学七年级（上）复习微专题精炼10 代数式及其求值

试卷更新日期：2023-10-26 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列各式符合代数式书写格式的为（）

A、 $b \div a$ B、 $a \times 4$ C、 $3 x - 2$ D、 $3 \frac{1}{2} x$

查看试题解析
2. 某企业今年一月份投入新产品的研发资金为a万元，以后每月投入新产品的研发资金与上月相比增长率都是20%．该厂今年三月份投入新产品的研发资金为b万元，则（）

A、 $b = a + 0.4$ B、 $b = 1.4 a$ C、 $b = 1.2 a$ D、 $b = 1.44 a$

查看试题解析
3. 某商场举行促销活动，促销的方法是“消费超过200元时，所购买的商品按原价打8折后，再减少20元”。若某商品的原价为x(x>200)元，则购买该商品实际付款的金额是（）

A、(80%x-20)元 B、80%(x-20)元 C、(20%x-20)元 D、20%(x-20)元

查看试题解析
4. 为落实“双减”政策，某校利用课后服务开展了主题为“书香满校园”的读书活动．现需购买甲、乙两种读本共100本供学生阅读，其中甲种读本的价格为10元/本，乙种读本的价格为8元/本，若购买甲种读本x本，则购买乙种读本的费用为（）

A、8x元 B、8(100-x)元 C、10(100-x)元 D、(100- 8x)元

查看试题解析
5. 下列各式中不能表示图中阴影部分面积的是（）

A、3(x+2)+x² B、x²+5x C、(x+3)(x+2)-2x D、x(x+3)+6

查看试题解析
6. 已知a是最大的负整数，b是绝对值最小的整数，c是最小的正整数，则|a+b-c|等于（）

A、-1 B、1 C、0 D、2

查看试题解析
7. 按如图所示的运算程序，能使输出 $y$ 值为 $5$ 的是（）

A、 $m = 2$ ， $n = 1$ B、 $m = 2$ ， $n = 0$ C、 $m = 2$ ， $n = 2$ D、 $m = 3$ ， $n = 2$

查看试题解析
8. 设(x-1)³=ax³+bx²+cx+d，则a-b+c-d的值为（）

A、2 B、8 C、-2 D、-8

查看试题解析
9. 若多项式2x²-x+6的值为8，则多项式9+2x-4x²的值是（）

A、13 B、11 C、5 D、-7

查看试题解析
10. 【阅读理解】计算：25×11＝275，13×11＝143，48×11＝528，74×11＝814，观察算式，我们发现两位乘11的速算方法：头尾一拉，中间相加，满十进一.
【拓展应用】已知一个两位数，十位上的数字是a，个位上的数字是b，这个两位数乘11，计算结果的十位上的数字可表示为（　　）

A、a或a＋1 B、a＋b或ab C、a＋b−10 D、a＋b或a＋b−10

查看试题解析

二、填空题

11. 若n-m=-3，则m-n= ， -1+m-n= ， 4-2m+2n=

查看试题解析
12. 当x=2时，代数式px³+qx+1的值为2 023，则当x=-2时，代数式px³+qx+1的值为

查看试题解析
13. 某通讯公司推出移动电话的两种计费方式：方式一：每月固定交费28元，月累计通话时间不超过120分，不再额外交费；当超过120分，超过部分每分加收0.12元．方式二：每月固定交费38元，月累计通话时间不超过180分，不再额外交费；当超过180分，超过部分每分加收0.10元．已知小王某个月累计通话的时间为t分（t＞180$）．
若按方式一计费，小王应缴费元；
若按方式二计费，小王应缴费元．

查看试题解析
14. 如图，表中的数据是按一定规律排列的，从中任意框出五个数字，若a，b，c，d，e表示框出的五个数字，请你用含a的式子表示a，b，c，d，e这五个数字的和为．

查看试题解析
15. 若x取任意值，等式 ${(x - 2)}^{4} = m_{0} x^{4} + m_{1} x^{3} + m_{2} x^{2} + m_{3} x + m_{4}$ 都成立，则有：

(1)、 $m_{4} =$ ；

(2)、 $m_{0} + m_{2} + m_{4} =$ .

查看试题解析

三、解答题

16. 已知 $a 、 b$ 互为相反数， $c 、 d$ 互为倒数， $x$ 的绝对值是3， $y$ 是最大的负整数，求 $2 x - c d + 6 (a + b) - | y |$ 的值．

查看试题解析
17. 如图是一个正方体纸盒的展开图，已知这个正方体纸盒相对两个面上的代数式的值相等．

(1)、求 $a$ ， $b$ ， $c$ 的值；

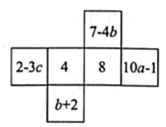(2)、求代数式 $b c - [2 a b - (3 a b c - b c) + 4 a b c]$ 的值．

查看试题解析
18. 为了提高居民的宜居环境，某小区规划修建一个广场（平面图如图中阴影部分所示）．

(1)、用含m，n的式子表示广场（阴影部分）的周长C和面积S；

(2)、若 $m = 30$ 米， $n = 20$ 米，修建每平方米需费用200元，求修建广场的总费用W的值．

查看试题解析
19. 将连续的奇数1，3，5，7，9，…，排列成如图所示数表：

(1)、十字框中的五个数的和与中间数23有什么关系？

(2)、设中间数为a，用式子表示十字框中五个数的和；

(3)、十字框中的五个数的和能等于2 015吗？能等于2 020吗？若能，请写出这五个数；若不能，请说明理由．

查看试题解析
20. 某商场销售一种西装和领带，西装每套定价1000元，领带每条定价200元.“国庆节”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案.
方案一：买一套西装送一条领带；
方案二：西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套，领带 $x$ 条（ $x > 20$ ）.

(1)、若该客户按方案一购买，需付款元.（用含 $x$ 的代数式表示）若该客户按方案二购买，需付款元.（用含 $x$ 的代数式表示）

(2)、若 $x = 40$ ，通过计算说明此时按哪种方案购买较为合算？

(3)、当 $x = 40$ 时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法及费用

查看试题解析
21. 历史上的数学巨人欧拉最先把关于x的多项式用记号f(x)的形式来表示，把x等于某数a时的多项式的值用f(a)来表示，例如当x=-1时，多项式f(x)=x²+3x-5的值记为，f(-1)，则f(-1)=(- 1)²+3x(-1)-5=-7．根据上述材料，解答下面的问题：

(1)、已知g (x)=- 2x²+3x-1，求g( $- \frac{1}{2}$ )的值．

(2)、已知f(x)=ax⁵+bx³+ 3x+c，且f(0)=-2．
①c= ▲
②若f(1)=-3，求a+b的值．
③若f(2)=11，求f(-2)的值．

查看试题解析
22. 阅读材料：我们知道，4x﹣2x+x＝（4﹣2+1）x＝3x，类似地，我们把（a+b）看成一个整体，则4（a+b）﹣2（a+b）+（a+b）＝（4﹣2+1）（a+b）＝3（a+b）．“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．
尝试应用：

(1)、把（a﹣b）²看成一个整体，合并3（a﹣b）²﹣6（a﹣b）²+2（a﹣b）²的结果是

(2)、已知x²﹣2y＝4，求3x²﹣6y﹣21的值；

(3)、已知a﹣2b＝3，2b﹣c＝﹣5，c﹣d＝10，求（a﹣c）+（2b﹣d）﹣（2b﹣c）的值．

查看试题解析