北师大版数学七年级(上)复习微专题精炼9 有理数的混合运算
试卷更新日期:2023-10-26 类型:复习试卷
一、选择题
-
1. 下列各式子中,不正确的是( )A、 B、 C、 D、2. 下列各式的运算中,不正确的是( )A、1+6×()÷(-6)= B、(-6)÷(-4)÷(+)= C、 D、3. 计算的结果是( )A、36 B、 C、6 D、4. 定义一种新运算: , 如 , 则的结果为( )A、 B、 C、 D、5. 小夕学习了有理数运算法则后,编了一个计算程序.当他输入任意一个有理数时,显示屏上出现的结果总等于所输入的有理数的3倍与的差.当他第一次输入 , 然后又将所得的结果再次输入后,显示屏上出现的结果应是( )A、 B、 C、 D、6. 按下图所示的程序运算:当输人的数据为-1时,输出的数据是( )
 A、2 B、4 C、6 D、87. 若成立,则“”中的运算符号是( )A、 B、 C、 D、8. 如果 互为相反数,互为倒数,m是最大的负整数,则的值是( )A、 B、 C、0 D、19. 时差的计算方法:两个时区标准时间(即时区数)相减就是时差,时区的数值大的时间早.比如中国北京是东八区(),美国纽约是西五区(),两地的时差是13小时,北京比纽约要早13个小时,如北京时间2月1日18:00时,美国纽约为2月1日5:00.若美国纽约时间为3月1日20:00时,埃及开罗时间为3月2日3:00,则开罗所在的时区是( )A、西二区 B、西三区 C、东二区 D、东三区10. 九宫格起源于中国古代的神秘图案河图和洛书.如图,将 , , , , , , , , 填入九宫格内,使每行、每列、每条对角线上三个数的和都相等,则的值为( )
A、2 B、4 C、6 D、87. 若成立,则“”中的运算符号是( )A、 B、 C、 D、8. 如果 互为相反数,互为倒数,m是最大的负整数,则的值是( )A、 B、 C、0 D、19. 时差的计算方法:两个时区标准时间(即时区数)相减就是时差,时区的数值大的时间早.比如中国北京是东八区(),美国纽约是西五区(),两地的时差是13小时,北京比纽约要早13个小时,如北京时间2月1日18:00时,美国纽约为2月1日5:00.若美国纽约时间为3月1日20:00时,埃及开罗时间为3月2日3:00,则开罗所在的时区是( )A、西二区 B、西三区 C、东二区 D、东三区10. 九宫格起源于中国古代的神秘图案河图和洛书.如图,将 , , , , , , , , 填入九宫格内,使每行、每列、每条对角线上三个数的和都相等,则的值为( )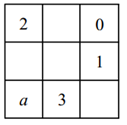 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 某长方体形状的容器长、宽、高分别为5cm,3cm,10cm,容器内原有水的高度为3cm,现准备向它继续注水. 用V(单位:cm3)表示新注入水的体积,则V的取值范围是 .12. 中百超市推出如下优惠方案:(1)一次性购物不超过100元,不享受优惠;(2)一次性购物超过100元,但不超过300元一律9折;(3)一次性购物超过300元一律8折,某人两次购物分别付款80元、252元,如果他将这两次所购商品一次性购买,则可节省13. 如果A表示最小的正整数,B表示最大的负整数,C表示绝对值最小的有理数,那么计算 .14. 整数a、b、c满足1000|a|+10|b|+|c|=2023,其中|a|>1且abc>1,则a+b+c的最小值是 .15. 甲、乙两人分别在A,B两条生产线上加工零件,在A生产线,甲、乙均是每天最少可以加工2个A零件.当连续生产时,甲第一天能加工10个A零件,每连续加工一天,加工的零件数比前一天少2个;乙第一天能加工8个A零件,每连续加工一天,加工的零件数比前一天少1个.在B生产线,甲每天加工7个B零件,乙每天加工8个B零件.在同一天内,甲和乙不能在同一条生产线上工作,且在一条生产线连续工作不少于3天时可改变生产线,改变生产线后加工时间重新计算.根据题意,得:(1)、甲在A生产线连续工作3天最多能加工A零件个;(2)、若一个A零件、一个B零件组成一套产品,则14天最多能加工套产品.
三、计算题
-
16. 计算(1)、(2)、(3)、(4)、 .(5)、(6)、(7)、(8)、 .17. 用简便方法计算:(1)、(2)、
四、综合题
-
18. 已知算式“”.(1)、嘉嘉将数字“5”抄错了,所得结果为 , 则嘉嘉把“5”错写成了;(2)、淇淇不小心把运算符号“×”错看成了“+”,求淇淇的计算结果比原题的正确结果大多少.19. 有个填写运算符号的游戏:在“1□2□6□9”中的每个□内,填入+,-,×,÷中的某一个(可重复使用),然后计算结果.(1)、计算:;(2)、若 , 请推算□内的符号;(3)、在“”的□内填入符号后,使计算所得数最小,直接写出这个最小数.20. 阅读以下材料,完成相关的填空和计算.(1)、根据倒数的定义我们知道,若 , 则 .(2)、计算 .(3)、根据以上信息可知: .21. 小明和小智在游戏中把五个相同的曲别针环环相扣,每个曲别针的长度为15毫米,厚度为1毫米,如果把这个曲别针环拉直(如图所示),则这个曲别针环拉直后长为多少呢?两位同学思考后分别给出了思路:

小明:如下图,我只要分别把后面的每段长度算出来,相加就可以;

小智:我采用的是平移的思想,先假设五个曲别针不是环环相扣,而是紧密排列成下图

此时总长为毫米,每两个曲别针环环相扣,相当于把右边的曲别针向左平移了一定的长度,然后用减去所有的平移长度就可以算出来了.
请完成下面的问题:
(1)、这个曲别针环长为毫米;(2)、请根据小智的思路列出相应的算式: .22. 某市计划修建一个长为米,宽为米的矩形市民休闲广场.(1)、请计算该广场的面积S(结果用科学记数法表示);(2)、如果用一种正方形大理石地砖铺装该广场地面,请计算需要多少块大理石地砖.23. 东方滴滴快车司机张师傅某天上午在东西走向的大街上连续接到六位客人(假设第一位客人下车后刚好第二位客人上车,以此类推),如果规定向东为正,向西为负,他这天上午行车里程(单位:千米)如下:-2,+10,-2,+8,-17,-3.(1)、将最后一位乘客送到目的地时,张师傅距出发地多远?此时在出发地东边还是西边?(2)、若汽车耗油量为0.1升/千米,这天上午张师傅共耗油多少升?(3)、若滴滴快车的起步价为10元,起步里程为3千米(包括3千米),超过部分每米2元,请问张师傅这天上午收入多少元?24. 今年以来,由于受国际天然气形势的影响,我国天然气市场总体呈现量紧价高的态势,为确保天然气保供稳价,提高居民生活用气的保障,某地决定从今年月开始调整居民用气价格,调整前后价格如下表(每月用气量为立方米):用气类别
第一档()
第二档()
第三档()
调整前
调整后
注:该地天然气收费按月实行阶梯收费
(1)、某用户月(调整前)缴天然气费元,求该用户这月用气量;(2)、若该用户月(调整后)用气量与月相同,则该用户月比月多缴费多少元?(3)、因天气转冷,该用户今年月因取暖用气量急剧增加,缴天然气费元,该用户今年月用气量是多少立方米?25. 规定:求若干个相同的不为零的有理数的除法运算叫做除方.如 , .类比有理数的乘方,我们把记作 , 读作“2的星3次方”;把记作 , 读作“的星4次方”.
一般地,把记作(其中, , , 为整数),读作“的星次方”.
(1)、直接写出计算结果: , , ;(2)、结合(1)中的运算,尝试把有理数的除方运算转化为乘方运算,可以归纳如下:一个非零有理数的星 , 为整数)次方等于 (从以下四个选项中选择最合适的一个,填写序号即可).
①这个数的相反数的次方;
②这个数的绝对值的次方;
③这个数的倒数的次方;
④这个数的次方.
(3)、关于“除方”运算,下列说法错误的是____ ;A、任何非零有理数的星3次方都等于它的倒数; B、对于任何不小于3正整数 , ; C、; D、负数的星5次方的结果是负数,负数的星6次方的结果是正数.(4)、结合上述探究结果,计算下式的值..