北师大版数学七年级（上）复习微专题精炼6 数轴

试卷更新日期：2023-10-26 类型：复习试卷

进入出卷网下载

一、选择题

1. 以下是四位同学画的数轴，其中正确的是（）

A、 B、 C、 D、

查看试题解析
2. 小明在写作业时不慎将一滴墨水滴在数轴上，根据图的数值，判断墨迹盖住的整数共有（）个．

A、11 B、9 C、10 D、8

查看试题解析
3. 如图所示，若数轴上的点A，B分别与有理数-2，2对应，用圆规在数轴上画点C，则与点C对应的有理数是（）

A、3 B、4 C、5 D、6

查看试题解析
4. a，b，c在数轴上的位置如下图所示，下列说法正确的是（）

A、a，b，c均表示正数 B、a，b，c 均表示负数 C、a，b表示正数，c表示负数 D、a，b表示负数，c表示正数

查看试题解析
5. 算式-3-5的结果对应图中的（）

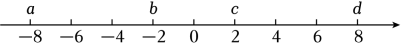A、a B、b C、c D、d

查看试题解析
6. 已知 a、b 在数轴上的位置如下所示，则 a、b、 $- a$ 、 $- b$ 的大小关系为（　　）

A、 $a > b > - a > - b$ B、 $a > - a > - b > b$ C、 $- b > a > - a > b$ D、 $- b > a > b > - a$

查看试题解析
7. 如图， $| a | - a$ 的值为（）

A、 $- 6$ B、 $0$ C、 $3$ D、 $6$

查看试题解析
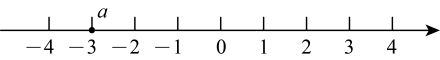8. 一电子跳蚤落在数轴上的某点k₀处，第一步从k₀向左跳一个单位到k₁ ，第二步从k₁向右跳2个单位到k₂ ，第三步由k₂处向左跳3个单位到k₃ ，第四步由k₃向右跳4个单位k₄ ， ….按以上规律跳了100步后，电子跳蚤落在数轴上的数是0，则k₀表示的数是

A、0 B、100 C、50 D、 $- 50$

查看试题解析
9. 已知数轴上的四点P，Q，R，S对应的数分别为p，q，r，s．且p，q，r，s．在数轴上的位置如图所示，若 $r - p = 6$ ， $s - p = 9$ ， $s - q = 7$ ，则 $r - q$ 等于（）

A、3 B、4 C、2 D、5

查看试题解析
10. 如图，圆的周长为4个单位长度．在该圆的4等分点处分别标上0、1、2、3，先让圆周上表示数字0的点与数轴上表示-1的点重合，再将数轴按逆时针方向环绕在该圆上．则数轴上表示2013的点与圆周上表示数字（）的点重合．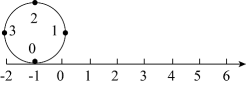

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

11. 数轴上点A表示的数是 $- 2$ ，将点A在数轴上平移4个单位长度得到点B ．则点B表示的数是．

查看试题解析
12. 如图1，点A ， B ， C是数轴上从左到右排列的三点，分别对应的数为 $- 4$ ， b ， 5．某同学将刻度尺如图2放置，使刻度尺上的数字0对齐数轴上的点A ，发现点B对齐刻度尺1.5cm处，点C对齐刻度尺4.5cm处．

图1 图2

(1)、在图1的数轴上， $A C =$ 个单位长度；

(2)、求数轴上点B所对应的数b为．

查看试题解析
13. 点 $M$ 在数轴上运动，先向右移动 $7$ 个单位长度，再向左移动 $4$ 个单位长度，此时正好在原点处， $M$ 开始运动时表示的数是．

查看试题解析
14. 已知：如图所示，A、B是数轴上的两个点，点A所表示的数为-5，动点P以每秒4个单位长度的速度从点B向左运动，同时，动点Q、M从点A向右运动，且点M的速度是点Q速度的 $\frac{1}{3}$ ，当运动时间为2秒和4秒时，点M和点P的距离都是6个单位长度，则当点P运动到点A时，动点Q所表示的数为.

查看试题解析
15. 电子青蛙落在数轴上的某一点 $P_{0}$ ，第一步从 $P_{0}$ 向左跳 $1$ 个单位到 $P_{1}$ ，第二步由 $P_{1}$ 向右跳 $2$ 个单位到 $P_{2}$ ，第三步由 $P_{2}$ 向左跳 $3$ 个单位到 $P_{3}$ ，第四步由 $P_{3}$ 向右跳 $4$ 个单位到 $P_{4}$ ， ……，按以上规律跳了 $20$ 步时，电子青蛙落在数轴上的点是 $10$ ，则电子青蛙的初始位置 $P_{0}$ 点所表示的数是．

查看试题解析

三、综合题

16. 有理数： $\frac{1}{3}$ ， $- 1$ ， $0$ ， $3 \frac{1}{2}$ ， $5$ ， $- 2 \frac{1}{2}$

(1)、请将以上各数填到相应的横线上：
①整数有：；
②非负数有：；

(2)、将上面各数在数轴上表示出来，并把这些数用“＜”连接.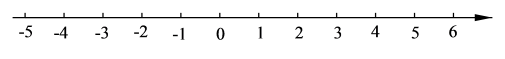

查看试题解析
17. 已知有理数a，b，其中数a在如图所示的数轴上对应点M，b是负数，且b在数轴上对应的点与原点的距离为3

(1)、a＝， b＝．

(2)、写出大于- $\frac{5}{2}$ 的所有负整数；

(3)、在数轴上标出表示- $\frac{5}{2}$ ， 0，-|-1|，-b的点，并用“＜“连接起来．

查看试题解析
18. 同学们都知道，|4-(-2)|表示4与-2的差的绝对值，实际上也可理解为4与-2两数在数轴上所对应的两点之间的距离；同理|x-3|也可理解为x与3两数在数轴上所对应的两点之间的距离.试探索：

(1)、|4-(-2)|=

(2)、若|x-2|=5，求x的值；

(3)、求|x-1|+|x+2|的最小值

查看试题解析
19. 如图，在数轴上点A表示数a，点B表示数b，点C表示数c，点A到点B的距离记为 $A B$ ，我们规定： $A B$ 的大小可以用位于右边的点表示的数减去左边的点表示的数表示，即 $A B = b - a$ .其中b是最大的负整数，a，c满足 $| a + 3 |$ 与 ${(c - 5)}^{2}$ 互为相反数.

(1)、 a= ， b= ， c=；

(2)、以某点D为折点，将此数轴向右对折，若点A在点C的右边，且 $A C = 2$ ，则D表示的数是；

(3)、若点A以每秒2个单位长度的速度向右运动t秒时， $5 A B = A C$ .求出t的值.

查看试题解析
20. 定义：若A，B，C为数轴上三点，若点C到点A的距离是点C到点B的距离2倍，我们就称点C是 $[A ， B]$ 的美好点.
例如；如图1，点A表示的数为 $- 1$ ，点B表示的数为2，表示1的点C到点A的距离是2，到点B的距离是1，那么点C是 $[A ， B]$ 的美好点；又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D就不是 $[A ， B]$ 的美好点，但点D是 $[B ， A]$ 的美好点.
如图2，M，N为数轴上两点，点M所表示的数为 $- 7$ ，点N所表示的数为2.

(1)、点E，F，G表示的数分别是-3，6.5，11，其中是 $[M ， N]$ 美好点的是；写出 $[N ， M]$ 美好点H所表示的数是.

(2)、现有一只电子蚂蚁P从点N开始出发，以2个单位每秒的速度向左运动.当t为何值时，点P恰好为M和N的美好点？

查看试题解析