北师大版数学七年级（上）复习微专题精炼5 有理数及运算

试卷更新日期：2023-10-26 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列7个数： $- \frac{7}{4}$ 、 $1.010010001$ 、 $\frac{4}{33}$ 、0、 $- π$ 、 $- 3.2626626662$ ……（两个2之间依次多一个6）、 $0.1 \dot{2}$ ，其中有理数有（　　）个．

A、3 B、4 C、5 D、6

查看试题解析
2. 一袋面粉的包装袋上标有“净含量： $25 \pm 0.2$ 千克”字样，下面不可能是这袋面粉的质量的是（）．

A、24.8千克 B、24.9千克 C、25.2千克 D、25.5千克

查看试题解析
3. 已知a，b，c为非零有理数，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值不可能为（）

A、0 B、-3 C、-1 D、3

查看试题解析
4. 两个有理数的和为正数，那么这两个数一定（）

A、都是正数 B、符号相同 C、有一个是 $0$ D、至少有一个正数

查看试题解析
5. 下列计算结果与－5－7的结果相同的是（）

A、－10－(－2) B、－10－2 C、－5＋7 D、5＋7

查看试题解析
6. 下列交换加数的位置的变形中，正确的是（　　）

A、 $1 - 4 + 4 - 5 = 1 - 4 + 5 - 4$ B、 $- \frac{1}{3} - \frac{1}{6} - \frac{1}{4} = \frac{1}{4} - \frac{1}{3} - \frac{1}{6}$ C、 $1 - 2 + 3 - 4 = 2 - 1 + 4 + 3$ D、 $4.5 - 1.7 - 2.5 + 1.8 = 4.5 - 2.5 + 1.8 - 1.7$

查看试题解析
7. 有理数 $a$ 、 $b$ 在数轴上的位置如图所示，则下列结论正确的是（）

A、 $\frac{a}{b} > 0$ B、 $a - b > 0$ C、 $a b > 0$ D、 $a + b < 0$

查看试题解析
8. 观察算式 $(- 4) \times \frac{1}{7} \times (- 25) \times 28$ 的过程中，能使运算变得简便的运算律是（）

A、直接运算 B、乘法结合律 C、乘法交换律和结合律 D、乘法对加法的分配律

查看试题解析
9. 与101×9.9计算结果相同的是（）

A、100×9.9＋1 B、100×9.9＋9.9 C、100×9＋100×0.9 D、100×9.9﹣9.9

查看试题解析
10. （1.25+1.25+1.25+1.25）×25×8，最简便的计算方法是（）

A、按顺序计算 B、（1.25×8）×（25×4） C、1.25×4×25×8 D、1.25×25×4×8

查看试题解析

二、填空题

11. 教育部门要求初中生每天睡眠时间应达到 $9$ 小时 $.$ 如果规定睡眠时间超过 $9$ 小时的记为正数，不足 $9$ 小时的记为负数，若小明同学某天的睡眠时间记为 $+ 0.4$ 小时，则小明同学的实际睡眠时间为小时．

查看试题解析
12. 绝对值小于4.99的所有整数的和是．

查看试题解析
13. 若 $a$ 、 $b$ 都是有理数，且 $b < 0$ ，则 $a$ ， $a - b$ ， $a + b$ 中最大的数是．

查看试题解析
14. 设a是最小的正整数，b是最大的负整数，c是绝对值最小的有理数，则a－b＋c ．

查看试题解析
15. － $\frac{3}{2}$ 的倒数是；绝对值等于4的数是．

查看试题解析

三、计算题

16.

(1)、1.2×（-1 $\frac{2}{3}$ ）；

(2)、（-2 $\frac{2}{9}$ ）÷（- $\frac{2}{3}$ ）×（- $\frac{3}{2}$ ）．

查看试题解析
17. 计算：

(1)、 $1.9 + (- 4.4) - (- 8.1) - (+ 5.6)$ ；

(2)、 $(- \frac{1}{2} - \frac{1}{6} + \frac{3}{4}) \times (- 36)$ ．

查看试题解析
18. 计算：

(1)、 $5 \frac{1}{4} - (- 2 \frac{2}{3}) + (- 3 \frac{1}{4}) - (+ 4 \frac{2}{3})$

(2)、 $(- \frac{3}{4} - \frac{5}{8} + \frac{9}{12}) \times (- 24)$

查看试题解析
19. 阅读下面解答过程：计算： $4 \frac{2}{3} + \frac{1}{5} - 12 - \frac{6}{5} + 6 \frac{1}{3}$
      $解：原式 = 4 \frac{2}{3} + \frac{1}{5} + (- 12) + (- \frac{6}{5}) + 6 \frac{1}{3}$   （第一步）
      $= (4 \frac{2}{3} + 6 \frac{1}{3}) + (- \frac{6}{5} + \frac{1}{5}) + (- 12)$ （第二步）
      $= 11 - 1 + (- 12)$ （第三步）
      $= 10 + (- 12)$ （第四步）
      $= - 2$ （第五步）

(1)、上面解题过程存在错误，是从第步开始错误的；

(2)、写出正确的解答过程．

查看试题解析

四、解答题

20. 把下列各数填入相应的大括号里： $- 7$ ， $- 0.5$ ， $- \frac{1}{3}$ ， 0， $- 98 %$ ， $8.7$ ， $2018$
负整数集合：{     ▲     …}；
非负数集合：{     ▲  …}；
正分数集合：{     ▲  …}；
负分数集合：{     ▲  …}．

查看试题解析
21. 已知 $m ， n$ 互为相反数， $a ， b$ 互为倒数， $x$ 的绝对值等于 $3$ ，则求 $| x | - (m + a b + n) x + a b$ 的值．

查看试题解析
22. 有理数 $a$ ， $b$ ， $c$ 在数轴上的位置如图所示，且表示数 $a$ 的点、数 $b$ 的点与原点的距离相等.

(1)、用“＞”“＜”或“＝”填空： $a + b$ 0， $a - c$ 0， $b - c$ 0；

(2)、化简 $| a + b | + | a - c | - | b | + | b - c |$ .

查看试题解析
23. 小刚设计了一个正方体包装盒的展开图，由于粗心少设计了其中一个盖子，请你把它补上，使其成为一个两面均有盖子的正方体盒子，并在补全的图中填入-2，4， $\frac{1}{3}$ ，0.25， $- \frac{1}{2}$ ，3，使得折成正方体的相对面上的两个数互为倒数.

查看试题解析
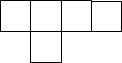24. 李强靠勤工俭学的收入维持上大学的费用．下面是他某一周的收支情况表（收入为正，支出为负，单位为元）
周一
周二
三
四
五
六
日
+15
+10
0
+20
+15
+10
+14
-8
-12
-19
-10
-9
-11
-8

(1)、到这个周末，李强有多少节余？

(2)、照这样，李强一个月（按30天计算）能有多少节余？

(3)、按以上的支出水平，李强一个月（按30天计算）至少有多少收入才能维持正常开支？

查看试题解析
25. 有一个水库某天8：00的水位为－0.1米(以警戒线为基准，记高于警戒线的水位为正)，在以后的6个时刻测得的水位升降情况如下(记上升为正，单位：米)：
0.5，－0.8，0，－0.2，－0.3，0.4．

(1)、经这6次水位升降后，水库的水位超过警戒线了吗？

(2)、现在由于下暴雨，水库水位以0.1米/小时速度上升，指挥部要求水位降至警戒线1米以下(含1米)，现在水库匀速泄水，可使静态水位按0.2米/小时速度下降，为达到指挥部最低要求，求水库需放水的时间．

查看试题解析
26. 小明早晨跑步，他从自己家出发，向东跑了2 $k m$ 到达小彬家，继续向东跑了1.5 $k m$ 到达小红家，然后又向西跑了4.5 $k m$ 到达学校，最后又向东，跑回到自己家．

(1)、若以小明家为原点，向东的方向为正方向，用1个单位长度表示1 $k m$ ，请在如图所示的数轴上，分别用点 $A ， B ， C$ 表示出小彬家，小红家和学校的位置；

(2)、小彬家与学校之间的距离为；

(3)、如果小明跑步的速度是200 $m / m i n$ ，那么小明跑步一共用了多长时间？

查看试题解析
27. 每个正方体相对两个面上写的数之和等于2．

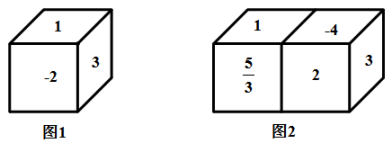(1)、求图1的正方体看不见的三个面上的数字的积．

(2)、现将两个这样的正方体黏合放置（如图2），求所有看不见的七个面上所写的数字的和．

查看试题解析
28. 下图是三个三角形，每个三角形的顶点处都有一个“O”，在每个“O”中填入一个数，满足这三个三角形的3个顶点处的“O”中的数的和都等于2．

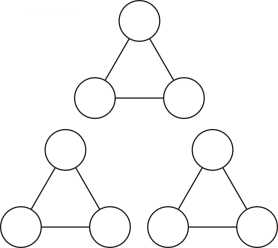(1)、将-8，-7，-6，-4，1，3，5，9，13这9个数填入恰当的位置，使得这三个三角形的3个顶点处的“O”中的数的和都等于2．

(2)、如果将(1)中的这9个数改为-13，-9，-5，-3，-1，4，6，7，8，还能满足要求吗？如果满足，请填在“O”中；如果不满足，请说明理由．

查看试题解析
29. 如图，有5张写着不同的数字的卡片，请你按要求借助卡片上的数字完成下列各题：

(1)、从中取出2张卡片，使卡片上的2个数的和最小，则和的最小值是多少？

(2)、从中取出2张卡片，使卡片上的2个数相乘的积最小，则积的最小值是多少？

(3)、再制作一张写有数字的卡片，使6张卡片上数字之和为0，则新做的卡片上数字应写多少？

查看试题解析

周一	周二	三	四	五	六	日
+15	+10	0	+20	+15	+10	+14
-8	-12	-19	-10	-9	-11	-8