安徽省六安市2023-2024学年八年级上学期数学第一次月考考试试卷
试卷更新日期:2023-10-26 类型:月考试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 在平面直角坐标系中,点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 在平面直角坐标系中,已知点 , ,平移线段 ,使点 落在点 处,则点 的对应点 的坐标为( )A、 B、 C、 D、3. 若正比例函数的图象经过点和点 , 当时, , 则的取值范围是( )A、 B、 C、 D、4. 如图所示,一次函数是常数,与正比例函数是常数,的图象相交于点 , 下列判断错误的是( )
 A、关于的方程的解是 B、关于的不等式的解集是 C、当时,函数的值比函数的值大 D、关于 , 的方程组 的解是5. 若一次函数的图象不经过第三象限,则的取值范围是( )A、 B、 C、 D、6. 某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间.出发时油箱中存油40升,到B地后发现油箱中还剩油4升,则从出发后到B地油箱中所剩油y(升)与时间t(小时)之间函数的大致图象是( )A、
A、关于的方程的解是 B、关于的不等式的解集是 C、当时,函数的值比函数的值大 D、关于 , 的方程组 的解是5. 若一次函数的图象不经过第三象限,则的取值范围是( )A、 B、 C、 D、6. 某人驾车从A地上高速公路前往B地,中途在服务区休息了一段时间.出发时油箱中存油40升,到B地后发现油箱中还剩油4升,则从出发后到B地油箱中所剩油y(升)与时间t(小时)之间函数的大致图象是( )A、 B、
B、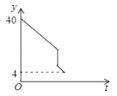 C、
C、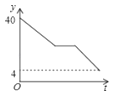 D、
D、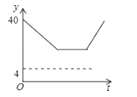 7. 已知 , 均为关于x的函数,当 时,函数值分别为 , ,若对于实数a,当 时,都有 ,则称 , 为亲函数,则以下函数 和 是亲函数的是( )A、 , B、 , C、 , D、 ,8. 象棋在中国有着三千多年的历史,如图是一方的棋盘,如果“帅”的坐标是(1,1),“卒”的坐标是(3,2),那么“马”的坐标是( )
7. 已知 , 均为关于x的函数,当 时,函数值分别为 , ,若对于实数a,当 时,都有 ,则称 , 为亲函数,则以下函数 和 是亲函数的是( )A、 , B、 , C、 , D、 ,8. 象棋在中国有着三千多年的历史,如图是一方的棋盘,如果“帅”的坐标是(1,1),“卒”的坐标是(3,2),那么“马”的坐标是( )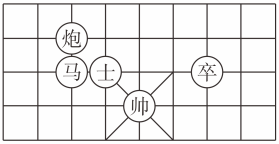 A、 B、 C、 D、9. 一次函数与正比例函数为常数,且),它们在同一坐标系中的大致图象是( )A、
A、 B、 C、 D、9. 一次函数与正比例函数为常数,且),它们在同一坐标系中的大致图象是( )A、 B、
B、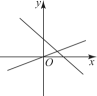 C、
C、 D、
D、 10. 如图,在平面直角坐标系中,的顶点坐标分别为 , , 若直线与至少有两个交点,则的取值范围是( )
10. 如图,在平面直角坐标系中,的顶点坐标分别为 , , 若直线与至少有两个交点,则的取值范围是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,共20.0分)
-
11. 函数y= 中自变量x的取值范围是 .12. 已知直线与直线平行,且经过点 , 则的值是 .13. 若一次函数y=2x+b与坐标轴围成的三角形面积为9,则这个一次函数的解析式为 .14. 如图,点在平面直角坐标系中按图中箭头所示方向运动,第次从原点运动到点 , 第次接着运动到点 , 第次接着运动到点 , 按这样的运动规律,经过第次运动后动点的坐标是 .

三、解答题(本大题共9小题,共90.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 已知A、B、C的坐标分别为试判断A、B、C三点是否在同一直线上,并说明理由.16. 如图,在平面直角坐标系中已知 , , , 把三角形先向左平移个单位长度,再向下平移个单位长度得到三角形 .
 (1)、写出 , , 三点的坐标;
(1)、写出 , , 三点的坐标;
(2)、画出三角形;
(3)、求三角形的面积.17. 已知与成正比例,且时, .(1)、求与之间的函数关系式;
(2)、当时,求的值.18. 已知:一次函数 .(1)、若一次函数的图象过原点,求实数m的值;(2)、当一次函数的图象经过第二、三、四象限时,求实数m的取值范围;(3)、当一次函数的图象不经过第三象限时,求实数m的取值范围.19. 某公交车每天的支出费用为元,每天的乘车人数人与每天利润利润票款收入支出费用元的变化关系如下表所示每位乘客的乘车票价固定不变:人
元
(1)、观察表中数据可知,若要保证不亏本,该公交车每天乘客应达到多少人?
(2)、请你估计一天乘客人数为人时,利润是多少?
(3)、写出与的关系表达式.20. 如图,已知直线与坐标轴交于 , 两点,直线与坐标轴交于 , 两点,两直线的交点为 . (1)、求 , , 的值;
(1)、求 , , 的值;
(2)、连接 , 试说明表示面积;
(3)、轴上存在点 , 使得 , 求出此时点的坐标.21. 某电信公司手机的A类收费标准如下:不管通话时间多长,每部手机每月必须缴月租费12元,另外,通话费按 元 计;B类收费标准如下:没有月租费,但通话费按 元 计 按照此类收费标准完成下列各题:(1)、直接写出每月应缴费用 元 与通话时长 分 之间的关系式:A类:B类:
(2)、若每月平均通话时长为300分钟,选择类收费方式较少.(3)、求每月通话多长时间时,按 两类收费标准缴费,所缴话费相等.22. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为 , 两车之间的距离为 , 图中的折线表示与之间的函数关系.根据图象进行以下探究: (1)、甲、乙两地之间的距为;
(1)、甲、乙两地之间的距为;
(2)、请解释图中点的实际意义;(3)、求慢车和快车的速度.23. 某校为达成省体育器材类装备,计划在京东惠购一次性购进篮球和足球共个,某电商内部信息表给出其进价与售价间的关系如表:篮球
足球
进价元个
售价元个
(1)、学校用元以进价购进这批篮球和足球,求购进篮球和足球各多少个;
(2)、设该电商所获利润为单位:元 , 购进篮球的个数为单位:个 , 请写出与之间的函数表达式不要求写出的取值范围;
(3)、因资金紧张,学校的进货成本只能在元的限额内,请为学校设计一种进货方案使得尽可能多地购买篮球和足球,同时要使电商利润最小;并求出利润的最小值.