云南省文山州文山市第二学区2023-2024学年八年级上学期数学月考考试试卷(9月)
试卷更新日期:2023-10-26 类型:月考试卷
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列四组数能作为直角三角形的三边长的是( )A、 , , B、 , , C、 , , D、 , ,2. 与数轴上的点一一对应的数是( )A、分数 B、有理数 C、无理数 D、实数3. 下列实数中,属于无理数的是( )A、 B、 C、 D、4. 下列各组数据中是勾股数的是( )A、 , , B、 , , C、 , , D、 , ,5. 估计的值( )A、在和之间 B、在和之间 C、在和之间 D、在和之间6. 下列各式中,错误的是( )A、 B、 C、 D、7. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、8.
如图,△ABC中,AB=AC,AD是∠BAC的平分线.已知AB=5,AD=3,则BC的长为( )
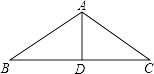 A、5 B、6 C、8 D、109. 若 , 为实数,且 , 则的值是( )A、 B、 C、 D、10. 如图在三角形中, , , 则点到线段的距离为( )
A、5 B、6 C、8 D、109. 若 , 为实数,且 , 则的值是( )A、 B、 C、 D、10. 如图在三角形中, , , 则点到线段的距离为( ) A、
A、
B、
C、
D、无法计算11. 若有意义,则的值可以是( )A、 B、 C、 D、12. 如图所示,在数轴上点所表示的实数是( ) A、
A、
B、
C、
D、二、填空题(本大题共4小题,共8.0分)
-
13. 计算: .14. 写一个无理数,使它与的积是有理数,这个无理数是 .15. 如图,以直角三角形的三边为边长分别作三个正方形,其中两个正方形的面积标示在图中,则字母所在的正方形的面积是 .
 16. 比较大小:填写“”或“” .
16. 比较大小:填写“”或“” .三、计算题(本大题共1小题,共6.0分)
-
17. 计算: .
四、解答题(本大题共7小题,共50.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 化简:(1)、(2)、19. 如图,长方体的底面边长分别为和 , 高为 , 如果用一根细线从点开始经过个侧面缠绕一圈到达点 , 那么所用细线最短需要多少?
 20. 一个数的两个平方根分别是与 , 若的立方根是 .
20. 一个数的两个平方根分别是与 , 若的立方根是 .
求:(1)、 , 的值;(2)、的立方根.21. 我校要对如图所示的一块地进行绿化,已知AD=4米,CD=3米,AD⊥DC,AB=13米,BC=12米,求这块地的面积.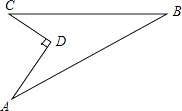
-


