四川省巴中市2023-2024学年九年级上学期数学月考考试试卷(9月)
试卷更新日期:2023-10-26 类型:月考试卷
一、选择题(本大题共12小题,共24.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 一元二次方程的二次项系数、一次项系数、常数项分别是( )A、 , , B、 , , C、 , , D、 , ,3. 方程的一般形式为( )A、 B、 C、 D、4. 已知关于的一元二次方程有一个非零根 , 则的值为( )A、 B、 C、 D、5. 用配方法解方程下列变形正确的是( )A、 B、 C、 D、6. 关于的方程有两个不相等的实数根,则的值范围是( )A、且 B、且 C、 D、7. 要组织一次排球邀请赛,参赛的每两个队之间比赛一场,根据场地和时间等条件,赛程计划安排天,每天安排场比赛,设比赛组织者应邀请个队参赛,则满足的关系式为( )A、 B、 C、 D、8. 三角形的一边长为 , 另两边长是方程的两个实数根,则这个三角形是( )A、等边三角形 B、等腰三角形 C、直角三角形 D、等腰直角三角形9. 若一元二次方程 无实数根,则一次函数的图象不经过第( )象限.A、四 B、三 C、二 D、一10. 一个三角形的两边长分别为和 , 第三边的边长是方程的根,则这个三角形的周长是( )A、 B、或 C、 D、以上选项都不正确11. 已知关于的一元二次方程 , 其中 , 在数轴上的对应点如图所示,则这个方程的根的情况是( )
 A、有两个不相等的实数根 B、有两个相等的实数根
A、有两个不相等的实数根 B、有两个相等的实数根
C、没有实数根 D、无法确定12. 对于两个不相等的实数、 , 我们规定符号表示、中较大的数,如:按照这个规定,方程的解为( )A、 , B、 ,
C、 D、二、填空题(本大题共6小题,共12.0分)
-
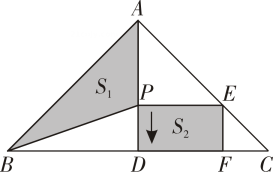
13. 已知是关于的一元二次方程的一个根,那么 .14. 关于的一元二次方程一个根是 , 则另一个根是 .15. 若方程有两个实数根,则的取值范围是 .16. 已知 , 则 .17. 设 是关于x的方程 的两个根,且 ,则 .18. 如图,在中, , , 为边上的高,动点从点出发,沿方向以的速度向点运动设的面积为 , 矩形的面积为 , 运动时间为 , 则 时, .
三、解答题(本大题共5小题,共64.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 解方程:
(1)、配方法
(2)、;
(3)、;
(4)、 .20. 关于的方程有两个不相等的实数根.(1)、求的取值范围.(2)、是否存在实数 , 使方程的两个实数根的倒数和等于?若存在,求出的值;若不存在,说明理由.21. 利用完全平方公式和的特点可以解决很多数学问题下面给出两个例子:
例、分解因式:
例、求代数式的最小值:
又
当时,代数式有最小值,最小值是 .
仔细阅读上面例题,模仿解决下列问题:(1)、分解因式:;(2)、代数式有最 大、小值,当 时,最值是 ;(3)、当、为何值时,多项式有最小值?并求出这个最小值.22. 某童装专卖店在销售中发现,一款童装每件进价为元,销售价为元时,每天可售出件为了迎接“六一”儿童节,商店决定采取适当的降价措施,以扩大销售量,增加利润据测算,每件童装每降价元,平均每天可多售出件.(1)、每件童装降价多少元时,平均每天盈利元.(2)、当童装销售价为多少元时,专卖店平均每天所获利润最大,最大为多少?23. 某校在基地参加社会实践活动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙墙足够长 , 另外三边用总长米的不锈钢栅栏围成,与墙平行的一边留一个宽为米的出入口,如图所示,如何设计才能使园地的面积最大?下面是两位学生争议的情境:
请根据上面的信息,解决问题:
(1)、设米 , 试用含的代数式表示的长;(2)、请你判断谁的说法正确,为什么?