安徽省六安市霍邱县2023-2024学年九年级上学期数学月考考试试卷(9月)
试卷更新日期:2023-10-26 类型:月考试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列函数中,属于关于的二次函数的是( )A、 B、
C、 D、2. 下列各点中,一定在反比例函数的图象上的点是( )A、 B、 C、 D、3. 抛物线的顶点坐标是( )A、 B、 C、 D、4. 若点在二次函数的图象上,则的值为( )A、 B、 C、 D、5. 已知 , , 都在双曲线上,则 , , 的大小关系是( )A、 B、 C、 D、6. 若抛物线是常数的顶点在轴上,则的值为( )A、 B、 C、或 D、或7. 已知二次函数 , 下列说法正确的是( )A、该函数图象开口向上
B、若点和都在该函数图象上,则
C、该函数图象与轴一定有交点
D、时,随的增大而减小8. 反比例函数是常数,且与二次函数在同一坐标系内的大致图象是( )A、 B、
B、
C、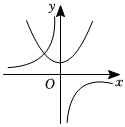 D、
D、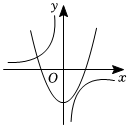 9. 在一次足球比赛中,某队守门员开出的球门球,经过第一次飞行后的落地点为 , 第二次从落地点反弹后继续向前飞行,落地点为 , 如图,已知第一次飞行经过秒时球距离地面的高度米适用公式 , 足球第二次飞行路线满足抛物线,且第二次飞行的最大高度和从反弹到落地所用时间均为第一次的一半,则足球第二次飞行所满足的函数表达式为( )
9. 在一次足球比赛中,某队守门员开出的球门球,经过第一次飞行后的落地点为 , 第二次从落地点反弹后继续向前飞行,落地点为 , 如图,已知第一次飞行经过秒时球距离地面的高度米适用公式 , 足球第二次飞行路线满足抛物线,且第二次飞行的最大高度和从反弹到落地所用时间均为第一次的一半,则足球第二次飞行所满足的函数表达式为( )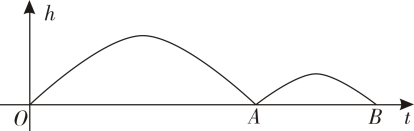 A、 B、
A、 B、
C、 D、10. 如图,抛物线为常数,且关于直线对称,与轴的其中一个交点坐标为下列结论中:;关于的一元二次方程的解是 , ;;其中不正确的个数是( )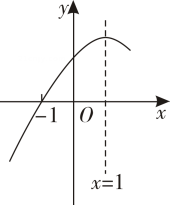 A、
A、
B、
C、
D、二、填空题(本大题共4小题,共20.0分)
-
11. 二次函数的二次项系数是 .12. 若抛物线与直线交于 , 两点,则点与点之间的距离 .13. 如图,在中, , , , 的顶点在轴的正半轴上,点 , 点在第一象限,且直角边平行于轴,反比例函数且的图象经过点和边的中点 , 则的值为 .
 14. 已知二次函数其中是常数,且 .(1)、若该函数的图象经过点 , 则的值为 ;(2)、若且当时对应的函数值均为正数,则的取值范围为 .
14. 已知二次函数其中是常数,且 .(1)、若该函数的图象经过点 , 则的值为 ;(2)、若且当时对应的函数值均为正数,则的取值范围为 .三、解答题(本大题共9小题,共90.0分。解答应写出文字说明,证明过程或演算步骤)
-
15. 已知是关于的二次函数,求的值.16. 已知二次函数是常数,且的图象的对称轴为直线 , 最大值为 , 且经过点 , 求 , , 的值.17. 如图,一辆宽为米的货车要通过跨度为米,拱高为米的单行抛物线隧道从正中通过 , 抛物线满足表达式保证安全,车顶离隧道的顶部至少要有米的距离,求货车的限高应是多少.
 18. 据物理学知识,一定的压力作用于物体上产生的压强与物体受力面积成反比例,已知当时, .
18. 据物理学知识,一定的压力作用于物体上产生的压强与物体受力面积成反比例,已知当时, .
(1)、试确定与之间的函数表达式;
(2)、如果作用于物体上的压力能产生的压强要大于时,求物体受力面积的取值范围.19. 已知二次函数与一次函数 .(1)、在给出的平面直角坐标系中画出这两个函数的图象. (2)、结合图象:
(2)、结合图象:
直接写出这两个函数图象的交点坐标;
直接写出对应的自变量的取值范围.20. 已知二次函数是常数 .(1)、求证:无论取何值,该函数的图象与轴一定有两个交点;
(2)、取一个你喜欢的的值,并求出此时函数图象与轴的交点坐标.21. 如图,在平面直角坐标系中,一次函数与反比例函数其中的图象相交于 , 两点.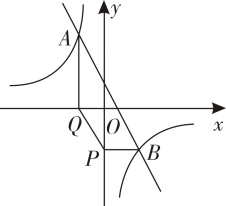 (1)、求一次函数与反比例函数的表达式;
(1)、求一次函数与反比例函数的表达式;
(2)、过点作轴,交轴于点 , 过点作交轴于点 , 连接 , 求四边形的面积.22. 如图,在平面直角坐标系中,二次函数的图象与轴交于 , 两点,与轴交于点 , 点在原点的左侧,点的坐标为 . (1)、求二次函数的表达式;
(1)、求二次函数的表达式;
(2)、若点是抛物线上一个动点,且在直线的上方连接 , , 并把沿翻折,得到四边形 , 是否存在点 , 使四边形为菱形?若存在,请求出此时点的坐标;若不存在,请说明理由.23. 某商店经销一种书包,已知这种书包的成本价为每个元市场调查发现,这种书包每天的销售量单位:个与销售单价单位:元有如下关系:设这种书包每天的销售利润为元.
(1)、求与之间的函数表达式;
(2)、这种书包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)、如果物价部门规定这种书包的销售单价不高于元;该商店销售这种书包每天要获得元的销售利润,销售单价应定为多少元?