山东省济南市章丘区2023-2024学年九年级上学期数学第一次月考考试试卷
试卷更新日期:2023-10-26 类型:月考试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 矩形具有而菱形不一定具有的性质是( )A、对角相等 B、对角线相等 C、对边相等 D、对角线互相平分2. 方程 的解是( )A、 B、 C、 D、无实数根3. 如图,把矩形ABCD沿EF对折,若∠1=50°,则∠AEF等于( )
 A、50° B、80° C、65° D、115°4. 已知方程的两根分别是和 , 则的值等于( )A、 B、 C、 D、5. 某公司今年月的营业额为万元,按计划第四季度的总营业额要达到万元,求该公司 , 两个月营业额的月平均增长率.设该公司 , 两个月营业额的月平均增长率为 , 则可列方程为( )A、 B、 C、 D、6. 三角形的两边长分别为和 , 第三边长为方程的一个根,则这个三角形的周长为( )A、 B、或 C、 D、7. 如图,在菱形中,菱形的边长为 , 对角线的长为 , 延长至 , 平分 , 点是上任意一点,则的面积为( )
A、50° B、80° C、65° D、115°4. 已知方程的两根分别是和 , 则的值等于( )A、 B、 C、 D、5. 某公司今年月的营业额为万元,按计划第四季度的总营业额要达到万元,求该公司 , 两个月营业额的月平均增长率.设该公司 , 两个月营业额的月平均增长率为 , 则可列方程为( )A、 B、 C、 D、6. 三角形的两边长分别为和 , 第三边长为方程的一个根,则这个三角形的周长为( )A、 B、或 C、 D、7. 如图,在菱形中,菱形的边长为 , 对角线的长为 , 延长至 , 平分 , 点是上任意一点,则的面积为( ) A、 B、 C、 D、8. 如图,在四边形中,、、、分别是边、、、的中点,则下列说法正确的是( )
A、 B、 C、 D、8. 如图,在四边形中,、、、分别是边、、、的中点,则下列说法正确的是( ) A、若四边形是平行四边形,则与相等 B、若四边形是正方形,则与互相垂直且相等 C、若 , 则四边形是矩形 D、若 , 则四边形是菱形9. 已知关于的一元二次方程无实数根,则的取值范围是( )A、 B、 C、 D、且10. 如图,菱形中, , 与交于点 , 为延长线上一点,且 , 连结 , 分别交 , 于点、 , 连结 , 则下列结论:
A、若四边形是平行四边形,则与相等 B、若四边形是正方形,则与互相垂直且相等 C、若 , 则四边形是矩形 D、若 , 则四边形是菱形9. 已知关于的一元二次方程无实数根,则的取值范围是( )A、 B、 C、 D、且10. 如图,菱形中, , 与交于点 , 为延长线上一点,且 , 连结 , 分别交 , 于点、 , 连结 , 则下列结论:;;由点、、、构成的四边形是菱形;其中正确的结论是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共24.0分)
-
11. 已知是方程的一个根,则的值是 .12. 已知是关于的一元二次方程,则 .13. 在数学活动课上,小明用四根长度相同的木条首尾相接制作了一个如图的正方形,而后将正方形的边固定,平推成图的图形,并测得 , 若图中的边长 , 则变形后图中图形的面积是 .
 14. 九年级班文学小组在举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,全组共互赠了本图书,则全组共有名同学.15. 正方形和正方形中,点在上, , , 是的中点,那么的长是 .
14. 九年级班文学小组在举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,全组共互赠了本图书,则全组共有名同学.15. 正方形和正方形中,点在上, , , 是的中点,那么的长是 . 16. 如图,中, , , , 点为边上任一点,过分别作于 , 于 , 则线段的最小值是 .
16. 如图,中, , , , 点为边上任一点,过分别作于 , 于 , 则线段的最小值是 .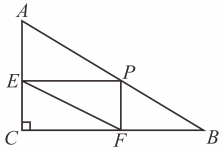
三、解答题
-
17. 某商城在年端午节期间促销海尔冰箱,每台进货价为元,标价为 .(1)、商城举行了“新老用户粽是情”摸奖活动,中奖者商城将冰箱连续两次降价,每次降价的百分率相同,最后以元售出,求每次降价的百分率;(2)、市场调研表明:当每台售价为元时,平均每天能售出台,当每台售价每降元时,平均每天就能多售出台,若商城要想使海尔冰箱的销售利润平均每天达到元,则每台冰箱的定价应为多少元?
四、解答题(本大题共9小题,共74.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 解下列方程:
(1)、;
(2)、 .19. 已知是关于的方程的一个根,求的值和方程的另一根.20. 在矩形中, , , 点从点出发向点运动到点即停止;同时点从点出发向点运动到点即停止,点、的速度都是 , 连结、、 , 设点、运动的时间为ts. (1)、当为何值时,四边形是矩形,请说明理由;(2)、当为何值时,四边形是菱形,请说明理由.21. 关于x的一元二次方程 有两个不相等的实数根x1 , x2.(1)、求实数m的取值范围;(2)、是否存在实数m,使得 成立?如果存在,求出m的值;如果不存在,请说明理由.22. 如图,在中,点是上一点,点是的中点,过点作交的延长线于点 .
(1)、当为何值时,四边形是矩形,请说明理由;(2)、当为何值时,四边形是菱形,请说明理由.21. 关于x的一元二次方程 有两个不相等的实数根x1 , x2.(1)、求实数m的取值范围;(2)、是否存在实数m,使得 成立?如果存在,求出m的值;如果不存在,请说明理由.22. 如图,在中,点是上一点,点是的中点,过点作交的延长线于点 . (1)、求证:;(2)、连接 , 如果点是的中点,那么当满足 时,四边形是菱形,请说明理由.23. 为培养学生正确的劳动价值观和良好的劳动品质某校为此规划出矩形苗圃苗圃的一面靠墙墙最大可用长度为米另三边用木栏围成,中间也用垂直于墙的木栏隔开分成面积相等的两个区域,并在如图所示的两处各留米宽的门门不用木栏 , 修建所用木栏总长米,设矩形的一边长为米.
(1)、求证:;(2)、连接 , 如果点是的中点,那么当满足 时,四边形是菱形,请说明理由.23. 为培养学生正确的劳动价值观和良好的劳动品质某校为此规划出矩形苗圃苗圃的一面靠墙墙最大可用长度为米另三边用木栏围成,中间也用垂直于墙的木栏隔开分成面积相等的两个区域,并在如图所示的两处各留米宽的门门不用木栏 , 修建所用木栏总长米,设矩形的一边长为米. (1)、矩形的另一边长为 米用含的代数式表示;(2)、矩形的面积能否为 , 若能,请求出的长;若不能,请说明理由.24. 如图,在菱形中,对角线 , 交于点 , 过点作的垂线,垂足为点 , 延长到点 , 使 , 连接 .
(1)、矩形的另一边长为 米用含的代数式表示;(2)、矩形的面积能否为 , 若能,请求出的长;若不能,请说明理由.24. 如图,在菱形中,对角线 , 交于点 , 过点作的垂线,垂足为点 , 延长到点 , 使 , 连接 .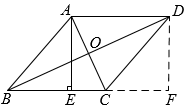 (1)、求证:四边形是矩形;(2)、若 , , 求的长.25. 阅读下列材料:利用完全平方公式,将多项式变形为的形式,然后由就可求出多项式的最小值.
(1)、求证:四边形是矩形;(2)、若 , , 求的长.25. 阅读下列材料:利用完全平方公式,将多项式变形为的形式,然后由就可求出多项式的最小值.
例题:求的最小值.
解: .
因为不论取何值,总是非负数,即 .
所以 .
所以当时,有最小值,最小值是 .
根据上述材料,解答下列问题:(1)、填空: .(2)、将变形为的形式,并求出的最小值.(3)、如图所示的第一个长方形边长分别是、 , 面积为;如图所示的第二个长方形边长分别是、 , 面积为试比较与的大小,并说明理由. 26. 知四边形和四边形均为正方形,连接、 , 直线与交于点 .
26. 知四边形和四边形均为正方形,连接、 , 直线与交于点 . (1)、如图 , 当点在上时,线段和的数量关系是 ,的度数为 .(2)、如图 , 将正方形绕点旋转任意角度请你判断中的结论是否仍然成立,并说明理由.
(1)、如图 , 当点在上时,线段和的数量关系是 ,的度数为 .(2)、如图 , 将正方形绕点旋转任意角度请你判断中的结论是否仍然成立,并说明理由.
(3)、若 , , 则正方形绕点旋转过程中,点、是否重合?若能,请直接写出此时线段的长;若不能,说明理由.
-