吉林省长春市榆树市红星三中2023-2024学年九年级上学期月考数学试卷(9月份)
试卷更新日期:2023-10-26 类型:月考试卷
一、选择题(共8小题,每题3分,共24分)
-
1. 若二次根式有意义,则下列各数符合要求的是( )A、8 B、9 C、10 D、42. 下列运算正确的是( )A、 B、 C、 D、3. 下列立体图形中,俯视图与主视图不同的是( )A、
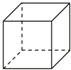 正方体
B、
正方体
B、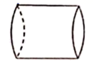 圆柱
C、
圆柱
C、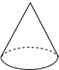 圆锥
D、
圆锥
D、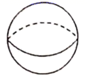 球
4. 下列事件为必然事件的是( )A、明天是晴天 B、任意掷一枚均匀的硬币100次,正面朝上的次数是50次 C、一个三角形三个内角和小于180° D、两个正数的和为正数5. 将抛物线y=2x2先向左平移3个单位长度,再向下平移2个单位长度,得到的抛物线的解析式是( )A、y=2(x-3)2-2 B、y=2(x+3)2-2 C、y=2(x-3)2+2 D、y=2(x+3)2+26. 下列各组线段中,成比例线段的一组是( )A、1,2,3,4 B、2,3,4,6 C、1,3,5,7 D、2,4,6,87. 如图,l1∥l2∥l3 , 直线AC、DF与这三条平行线分别交于点A、B、C和点D、E、F,若AB=4,DE=3,EF=6,则AC的长是( )
球
4. 下列事件为必然事件的是( )A、明天是晴天 B、任意掷一枚均匀的硬币100次,正面朝上的次数是50次 C、一个三角形三个内角和小于180° D、两个正数的和为正数5. 将抛物线y=2x2先向左平移3个单位长度,再向下平移2个单位长度,得到的抛物线的解析式是( )A、y=2(x-3)2-2 B、y=2(x+3)2-2 C、y=2(x-3)2+2 D、y=2(x+3)2+26. 下列各组线段中,成比例线段的一组是( )A、1,2,3,4 B、2,3,4,6 C、1,3,5,7 D、2,4,6,87. 如图,l1∥l2∥l3 , 直线AC、DF与这三条平行线分别交于点A、B、C和点D、E、F,若AB=4,DE=3,EF=6,则AC的长是( ) A、4 B、6 C、8 D、128. 某学校生物兴趣小组在该校空地上围了一块面积为200m2的矩形试验田,用来种植蔬菜.如图,试验田一面靠墙,墙长35m,另外三面用49m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).设试验田垂直于墙的一边AB的长为xm,则下列所列方程正确的是( )
A、4 B、6 C、8 D、128. 某学校生物兴趣小组在该校空地上围了一块面积为200m2的矩形试验田,用来种植蔬菜.如图,试验田一面靠墙,墙长35m,另外三面用49m长的篱笆围成,其中一边开有一扇1m宽的门(不包括篱笆).设试验田垂直于墙的一边AB的长为xm,则下列所列方程正确的是( ) A、x(49+1-x)=200 B、x(49-2x)=200 C、x(49+1-2x)=200 D、x(49-1-2x)=200
A、x(49+1-x)=200 B、x(49-2x)=200 C、x(49+1-2x)=200 D、x(49-1-2x)=200二、填空题(每题3分共18分)
-
9. 计算的结果是 .10. 要使有意义,则a的取值范围是 .11. 若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根,则m的值为 .12. 在△ABC中,∠C=90°,sinA= , 则tanB= .
13. 已知抛物线y=-3x2+bx+c经过点A(0,2)、B(4,2),则不等式-3x2+bx+c<2的解集是 .14. 如图所示,在△ABC中,BC>AC,点D在BC上,DC=AC=10,且 , 作∠ACB的平分线CF交AD于点F,CF=8,E是AB的中点,连接EF,则EF的长为 .
三、解答题(共78分)
-
15. 计算: .16. 解方程:2x2+4x-1=0(用配方法).17. 计算:cos30°-2(π-1)0+()-1-tan60°.18. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好.
 (1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)19. 如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=50°,∠APD=80°.
(1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)19. 如图,在⊙O中,直径AB与弦CD相交于点P,∠CAB=50°,∠APD=80°.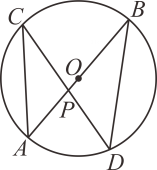 (1)、求∠B的度数;(2)、若BD=6,求直径AB的长.20. 如图,边长为1的小正方形组成了网格,点A、B均是格点,请你仅用无刻度的直尺画出满足下列条件的点P,并在图中标出点P.
(1)、求∠B的度数;(2)、若BD=6,求直径AB的长.20. 如图,边长为1的小正方形组成了网格,点A、B均是格点,请你仅用无刻度的直尺画出满足下列条件的点P,并在图中标出点P. (1)、图①中,点P为AB的中点;(2)、图②中,点P在线段AB上且AP=AB.21. 如图,四边形ABCD∽四边形A'B'C'D'.
(1)、图①中,点P为AB的中点;(2)、图②中,点P在线段AB上且AP=AB.21. 如图,四边形ABCD∽四边形A'B'C'D'. (1)、∠B=°.(2)、求边x,y的长度.22. 实数a、b在数轴上的位置如图所示.化简 .
(1)、∠B=°.(2)、求边x,y的长度.22. 实数a、b在数轴上的位置如图所示.化简 .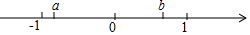 23. 小慧用因式分解法解一元二次方程2x(2x-1)=3(2x-1)时,她的做法如下:
23. 小慧用因式分解法解一元二次方程2x(2x-1)=3(2x-1)时,她的做法如下:方程两边同时除以(2x-1),得2x=3,(第一步)
系数化为1,得 . (第二步)
(1)、小慧的解法是不正确的,她从第 步开始出现了错误.(2)、请用小慧的方法完成这个题的解题过程.24. 某药品经过两次降价,每瓶零售价由56元降为31.5元.已知两次降价的百分比相同,求每次降价的百分率是多少.25. 如图,某中学有一块长30m,宽20m的矩形空地,计划在这块空地面积的一半区域种花,其余部分硬化.小亮同学设计了一个宽度相同的“U”形区域,求花带的宽度. 26. 点P(x,y)为平面直角坐标系中的任意一点,记m(x,y分别为点P的横、纵坐标),把m称为点P的特征数.
26. 点P(x,y)为平面直角坐标系中的任意一点,记m(x,y分别为点P的横、纵坐标),把m称为点P的特征数. (1)、当点P的坐标为(-2,2)时,求m的值.(2)、若点M(a,b)的特征数是5,点N(3a,b)的特征数是6,求点M的坐标.(3)、如图,在平面直角坐标系中,▱ABCD的顶点A、B、C的坐标分别为(3,2)、(4,4)、(3,6).
(1)、当点P的坐标为(-2,2)时,求m的值.(2)、若点M(a,b)的特征数是5,点N(3a,b)的特征数是6,求点M的坐标.(3)、如图,在平面直角坐标系中,▱ABCD的顶点A、B、C的坐标分别为(3,2)、(4,4)、(3,6).①点D的坐标为 ▲ .
②当m=5且点P(x,y)在▱ABCD内部(不包含边界)时,直接写出x的取值范围.
③当点P(x,y)在▱ABCD内部(不包含边界)时,直接写出m的取值范围.