四川省成都市四川大学附中新城分校2023-2024学年九年级上学期月考数学试卷(9月份)
试卷更新日期:2023-10-26 类型:月考试卷
一、单选题
-
1. 下列图形是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列方程中,是关于的一元二次方程的是( )A、 B、 C、 D、3. 用配方法解方程 时,原方程应变形为( )A、 B、 C、 D、4. 一元二次方程 的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根5. 如图,把一个长方形纸片沿折叠后,点、分别落在、的位置,若 , 则等于( )
2. 下列方程中,是关于的一元二次方程的是( )A、 B、 C、 D、3. 用配方法解方程 时,原方程应变形为( )A、 B、 C、 D、4. 一元二次方程 的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根5. 如图,把一个长方形纸片沿折叠后,点、分别落在、的位置,若 , 则等于( )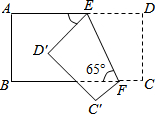 A、 B、 C、 D、6. 如图,下列条件之一能使平行四边形ABCD是菱形的为( )
A、 B、 C、 D、6. 如图,下列条件之一能使平行四边形ABCD是菱形的为( )①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
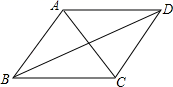 A、①③ B、②③ C、③④ D、①②③7. 如图,在▱中,对角线 , 相交于点 , 点 , 分别是 , 的中点,连接、 , 若 , , 则▱的周长为( )
A、①③ B、②③ C、③④ D、①②③7. 如图,在▱中,对角线 , 相交于点 , 点 , 分别是 , 的中点,连接、 , 若 , , 则▱的周长为( ) A、 B、 C、 D、8. 如图,已知中,于点 , 以点为中心,取旋转角等于 , 把顺时针旋转,得到 , 连接若 , , 则的大小为( )
A、 B、 C、 D、8. 如图,已知中,于点 , 以点为中心,取旋转角等于 , 把顺时针旋转,得到 , 连接若 , , 则的大小为( )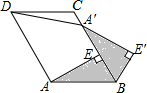 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若关于的一元二次方程有实数根,则的取值范围是 .10. 一元二次方程配方后化为 .11. 已知菱形的周长等于 , 一条对角线长为 , 则此菱形的面积为 .12. 如图,四边形ABCD是平行四边形,以点B为圆心,BC的长为半径作弧交AD于点E , 分别以点C , E为圆心,大于 的长为半径作弧,两弧交于点P , 作射线BP交AD的延长线于点F , ∠CBE=60°,BC=6,则BF的长为
 13. 如图,已知正方形的边长为 , 为边上一点,以点为中心,把顺时针旋转 , 得 , 连接 , 则的长等于 .
13. 如图,已知正方形的边长为 , 为边上一点,以点为中心,把顺时针旋转 , 得 , 连接 , 则的长等于 .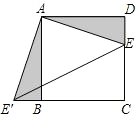
三、解答题
-
14. 用适当的方法解方程:(1)、;(2)、 .15. 若、是关于的方程的两个根,且求的值.16. 数形结合是解决数学问题的重要思想方法,在学习“因式分解”时,我们可以借助直观、形象的几何模型来求解下面共有三种卡片:型卡片是边长为的正方形;型卡片是长为 , 宽为的长方形;型卡片是边长为的正方形.
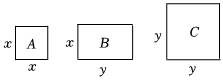 (1)、用张型卡片,张型卡片拼成如图的图形,根据图 , 多项式因式分解的结果为 ;
(1)、用张型卡片,张型卡片拼成如图的图形,根据图 , 多项式因式分解的结果为 ; (2)、请用张型卡片,张型卡片,张型卡片拼成一个大正方形,在图的虚线框中画出正方形的示意图,再据此写出一个多项式的因式分解.
(2)、请用张型卡片,张型卡片,张型卡片拼成一个大正方形,在图的虚线框中画出正方形的示意图,再据此写出一个多项式的因式分解. 17. 如图,在▱中,点 , 在对角线上,且 , 连接 , , , .
17. 如图,在▱中,点 , 在对角线上,且 , 连接 , , , .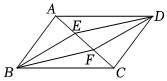 (1)、求证:四边形是平行四边形;(2)、若 , , , 求的度数.18. 如图 , 在中, , , 点是边上一动点,将线段绕点逆时针旋转得到 , 连接 .
(1)、求证:四边形是平行四边形;(2)、若 , , , 求的度数.18. 如图 , 在中, , , 点是边上一动点,将线段绕点逆时针旋转得到 , 连接 .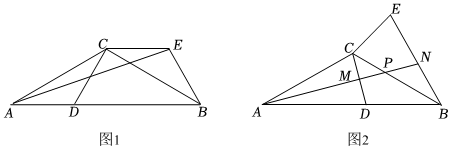 (1)、求的度数;(2)、连接 , 若 , , 求线段的长;(3)、如图 , 若 , , 点为中点,的延长线与交于点 , 与交于点 , 求线段的长.
(1)、求的度数;(2)、连接 , 若 , , 求线段的长;(3)、如图 , 若 , , 点为中点,的延长线与交于点 , 与交于点 , 求线段的长.四、填空题
-
19. 已知: , 则 .20. 如图所示,点为等边三角形内的一点, , , , 则的度数是 度.
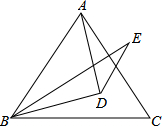 21. 如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是 .
21. 如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点落在A点,两条直角边分别与CD交于点F,与CB延长线交于点E.则四边形AECF的面积是 .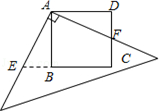 22.
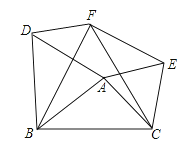
22.如图,在△ABC中,AB=4,AC=3,BC=5,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为
 23. 在平面直角坐标系xOy中,点A、B分别在x轴、y轴的正半轴上运动,点M为线段AB的中点.点D、E分别在x轴、y轴的负半轴上运动,且DE=AB=10.以DE为边在第三象限内作正方形DGFE,则线段MG长度的最大值为 .
23. 在平面直角坐标系xOy中,点A、B分别在x轴、y轴的正半轴上运动,点M为线段AB的中点.点D、E分别在x轴、y轴的负半轴上运动,且DE=AB=10.以DE为边在第三象限内作正方形DGFE,则线段MG长度的最大值为 .
五、解答题
-
24. 恒利商厦九月份的销售额为200万元,十月份的销售额下降了20%,商厦从十一月份起加强管理,改善经营,使销售额稳步上升,十二月份的销售额达到了193.6万元,求这两个月的平均增长率.25. 已知,矩形中.
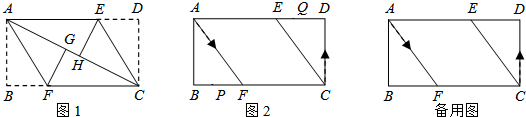 (1)、如图 , 分别沿、将两侧纸片折叠,使点、分别落在上的、处,则四边形为 形;(2)、如图 , 在矩形中,≌ , , , , 动点、分别从、两点同时出发,点自停止,点自停止.
(1)、如图 , 分别沿、将两侧纸片折叠,使点、分别落在上的、处,则四边形为 形;(2)、如图 , 在矩形中,≌ , , , , 动点、分别从、两点同时出发,点自停止,点自停止.若点的速度为每秒 , 点的速度为每秒 , 设运动时间为秒.当点在上运动,而点在上运动时,若四边形是平行四边形,求此时的值.
若点、的运动路程分别为、单位: , , 若四边形是平行四边形,求与满足的数量关系式.
26. 如图 , 在平面直角坐标系中,直线分别与轴,轴交于点 , , 过点作轴的垂线,与直线交于点 .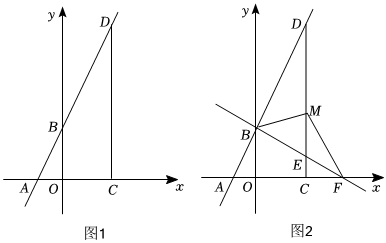 (1)、求点的坐标;(2)、点是线段上一动点,直线与轴交于点 .
(1)、求点的坐标;(2)、点是线段上一动点,直线与轴交于点 .若的面积为 , 求点的坐标;
如图 , 当点在轴正半轴上时,将直线绕点逆时针旋转后的直线与线段交于点 , 连接 , 若 , 求线段的长.