山东省济宁市汶上县2023-2024学年九年级上学期第一次质检数学试卷

试卷更新日期：2023-10-26 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. 方程 $2 x^{2} - 6 x = 9$ 的二次项系数、一次项系数、常数项分别为（）

A、 $6$ ， $2$ ， $9$ B、 $2$ ， $- 6$ ， $9$ C、 $2$ ， $- 6$ ， $- 9$ D、 $- 2$ ， $6$ ， $9$

查看试题解析
2. 下列各式中， $y$ 是 $x$ 的二次函数的为（）

A、 $y = - 9 + x^{2}$ B、 $y = - 2 x + 1$ C、 $y = \sqrt{x^{2} + 4}$ D、 $y = - (x + 1) + 3$

查看试题解析
3. 一元二次方程 $x^{2} - 6 x - 6 = 0$ 配方后化为（）

A、 ${(x - 3)}^{2} = 15$ B、 ${(x - 3)}^{2} = 3$ C、 ${(x + 3)}^{2} = 15$ D、 ${(x + 3)}^{2} = 3$

查看试题解析
4. 若关于 $x$ 的一元二次方程 $a x^{2} + b x + 6 = 0$ 的一个根为 $x = - 2$ ，则代数式 $6 a - 3 b + 6$ 的值为（）

A、9 B、 $- 3$ C、0 D、3

查看试题解析
5. 已知关于 $x$ 的方程 $(a - 1) x^{2} - 2 x + 1 = 0$ 有实数根，则 $a$ 的取值范围是（）

A、 $a \leq 2$ B、 $a > 2$ C、 $a \leq 2$ 且 $a \neq 1$ D、 $a < - 2$

查看试题解析
6. 某品牌网上专卖店1月份的营业额为50万元，已知第一季度的总营业额共600万元，如果平均每月增长率为x ，则由题意列方程应为（）

A、 $50 {(1 + x)}^{2} = 600$ B、 $50 [1 + (1 + x) + (1 + x)^{2}] = 600$ C、 $50 + 50 \times 3 x = 600$ D、 $50 + 50 \times 2 x = 600$

查看试题解析
7. 已知 $3$ 是关于 $x$ 的方程 $x^{2} - (m + 1) x + 2 m = 0$ 的一个实数根，并且这个方程的两个实数根恰好是等腰 $△ A B C$ 的两条边的边长，则 $△ A B C$ 的周长为（）

A、 $7$ B、 $10$ C、 $11$ D、 $10$ 或 $11$

查看试题解析
8. 抛物线 $y = 3 x^{2}$ 向右平移1个单位，再向下平移2个单位，所得到的抛物线是（）

A、 $y = 3 {(x - 1)}^{2} - 2$ B、 $y = 3 {(x + 1)}^{2} - 2$ C、 $y = 3 {(x + 1)}^{2} + 2$ D、 $y = 3 {(x - 1)}^{2} + 2$

查看试题解析
9. 如图，某小区计划在一块长为 $32 m$ ，宽为 $20 m$ 的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为 $570 m^{2} .$ 设道路的宽为 $x m$ ，则下面所列方程正确的是（）

A、 $(32 - x) (20 - x) = 32 \times 20 - 570$ B、 $32 x + 2 \times 20 x = 32 \times 20 - 570$ C、 $(32 - 2 x) (20 - x) = 570$ D、 $32 x + 2 \times 20 x - 2 x^{2} = 570$

查看试题解析
10. 若 $m$ 、 $n$ 是方程 $x^{2} - 2019 x - 1 = 0$ 的根，则 $(m^{2} - 2019 m + 3) \cdot (n^{2} - 2019 n + 4)$ 的值为（）

A、 $16$ B、 $12$ C、 $20$ D、 $30$

查看试题解析

二、填空题（本大题共5小题，共15.0分）

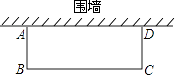
11. 方程 $2 x^{2} = - 3 x + 1$ 化为一般形式（二次项系数为正）是．

查看试题解析
12. 若 $(m + 1) x^{m (m - 2) - 1} + 2 m x - 1 = 0$ 是关于 $x$ 的一元二次方程，则 $m$ 的值是．

查看试题解析
13. 设 $x_{1}$ 、 $x_{2}$ 是方程 $5 x^{2} - 3 x - 2 = 0$ 的两个实数根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值为．

查看试题解析
14. 如图，邻边不等的矩形花圃ABCD，它的一边AD利用已有的围墙，另外三边所围的栅栏的总长度是6m．若矩形的面积为4m² ，则AB的长度是 m（可利用的围墙长度超过6m）．

查看试题解析
15. 有一个两位数，它的十位上的数字比个位上的数字小 $2$ ，十位上的数字与个位上的数字的积的 $3$ 倍刚好等于这个两位数，这个两位数为．

查看试题解析

三、解答题（本大题共7小题，共55.0分。解答应写出文字说明，证明过程或演算步骤）

16. 用适当的方法解方程：

(1)、 $(3 x + 2)^{2} = 25$ ；

(2)、 $3 x^{2} - 1 = 4 x$ ；

(3)、 $(2 x - 1)^{2} = 3 (2 x + 1)$ ；

(4)、 $x^{2} - 7 x + 10 = 0$ ．

查看试题解析
17. 已知关于 $x$ 的方程 $x^{2} + (2 k - 1) x + k^{2} - 1 = 0$ 有两个实数根 $x_{1}$ ， $x_{2}$ ．

(1)、求实数 $k$ 的取值范围；

(2)、若 $x_{1}$ ， $x_{2}$ 满足 $x_{1}^{2} + x_{2}^{2} = 16 + x_{1} x_{2}$ ，求实数 $k$ 的值．

查看试题解析
18. 某村 $2018$ 年的人均收入为 $20000$ 元， $2020$ 年的人均收入为 $24200$ 元．

(1)、求 $2018$ 年到 $2020$ 年该村人均收入的年平均增长率；

(2)、假设 $2021$ 年该村人均收入的增长率与前两年的年平均增长率相同，请你预测 $2021$ 年该村的人均收入是多少元？

查看试题解析
19. 如图，在一块长为 $30 m$ ，宽为 $20 m$ 的矩形地面上，要修建两横两竖的道路 $($ 横竖道路各与矩形的一条边平行 $)$ ，横、竖道路的宽度比为 $2$ ： $3$ ，剩余部分种上草坪，如果要使草坪的面积是地面面积的四分之一，应如何设计道路的宽度？

查看试题解析
20. 商场某种商品平均每天可销售30件，每件盈利50元，为了尽快减少库存，商场决定采取适当的降价措施．经调査发现，每件商品每降价1元，商场平均每天可多售出2件．

(1)、若某天该商品每件降价3元，当天可获利多少元？

(2)、设每件商品降价x元，则商场日销售量增加件，每件商品，盈利元(用含x的代数式表示)；

(3)、在上述销售正常情况下，每件商品降价多少元时，商场日盈利可达到2000元？

查看试题解析
21. 为解方程 $(x^{2} - 1)^{2} - 5 (x^{2} - 1) + 4 = 0$ ，我们可以将 $x^{2} - 1$ 视为一个整体，然后设 $x^{2} - 1 = y$ ，则
$(x^{2} - 1) 2 = y^{2}$ ，原方程化为 $y^{2} - 5 y + 4 = 0 . ①$
解得 $y_{1} = 1$ ， $y_{2} = 4$
当 $y = 1$ 时， $x^{2} - 1 = 1 . ∴ x^{2} = 2 . ∴ x = \pm \sqrt{2}$ ；
当 $y = 4$ 时， $x^{2} - 1 = 4$ ， $∴ x^{2} = 5$ ， $∴ x = \pm \sqrt{5}$ ．
$∴$ 原方程的解为 $x_{1} = \sqrt{2}$ ， $x_{2} = - \sqrt{2}$ ， $x_{3} = \sqrt{5}$ ， $x_{4} = - \sqrt{5}$
解答问题：

(1)、填空：在由原方程得到方程 $①$ 的过程中，利用法达到了降次的目的，体现了的数学思想．

(2)、解方程： $x^{4} - x^{2} - 6 = 0$ ．

查看试题解析
22. 如图，在 $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 5 c m$ ， $B C = 7 c m .$ 动点 $P$ 、 $Q$ 分别从点 $A$ ， $B$ 同时出发，点 $P$ 以 $1 c m / s$ 的速度向点 $B$ 移动，点 $Q$ 以 $2 c m / s$ 的速度向点 $C$ 移动． $($ 不考虑起始位置，且点 $P$ ， $Q$ 不与点 $A$ ， $B$ 重合 $)$

(1)、 $P$ 、 $Q$ 两点出发后第几秒时， $△ P B Q$ 的面积为 $4 c m^{2}$ ？

(2)、 $P$ 、 $Q$ 两点出发后第几秒时， $P Q$ 的长度为 $5 c m$ ；

(3)、 $△ P B Q$ 的面积能否为 $7 c m^{2}$ ？说明理由．

查看试题解析