山西省临汾市两县一市2023-2024学年八年级上学期数学月考考试试卷（9月）

试卷更新日期：2023-10-25 类型：月考试卷

进入出卷网下载

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1. $64$ 的立方根等于（）

A、 $4$ B、 $- 4$ C、 $8$ D、 $- 8$

查看试题解析
2. 下列各数中，是无理数的是（）

A、3.1415 B、 $\sqrt{4}$ C、 $\frac{22}{7}$ D、 $\sqrt{6}$

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{(- 3)^{2}} = - 3$ B、 $\sqrt{36} = \pm 6$ C、 $\sqrt[3]{9} = 3$ D、 $- \sqrt[3]{- 8} = 2$

查看试题解析
4. 若 $3^{x} = 15$ ， $3^{y} = 5$ ，则 $3^{x - y}$ 等于（）

A、 $5$ B、 $3$ C、 $15$ D、 $10$

查看试题解析
5. 若 $3 \times 3^{2 m} \times 3^{3 m} = 3^{11}$ ，则 $m$ 的值为（）

A、 $2$ B、 $3$ C、 $4$ D、 $5$

查看试题解析
6. 下列计算，正确的是（）

A、 $a^{2} \cdot a^{2} = 2 a^{2}$ B、 $a^{2} + a^{2} = a^{4}$
C、 $(- a^{2})^{2} = a^{4}$ D、 $(a + 1)^{2} = a^{2} + 1$

查看试题解析
7. 计算： ${(- \frac{2}{3} x^{2} y)}^{3} =$ （）

A、 $- 2 x^{6} y^{3}$ B、 $\frac{8}{27} x^{6} y^{3}$ C、 $- \frac{8}{27} x^{5} y^{3}$ D、 $- \frac{8}{27} x^{6} y^{3}$

查看试题解析
8. 若 $a - b = 8$ ， $a^{2} - b^{2} = 72$ ，则 $a + b$ 的值为（）

A、 $9$ B、 $- 9$ C、 $27$ D、 $- 27$

查看试题解析
9. 若 $m + n = 3$ ，则 $2 m^{2} + 4 m n + 2 n^{2} - 6$ 的值为（）

A、12 B、6 C、3 D、0

查看试题解析
10. 计算 $(\frac{2}{3})^{2017} \times 1 . 5^{2016} \times (- 1)^{2017}$ 的结果是（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $- \frac{2}{3}$ D、 $- \frac{3}{2}$

查看试题解析

二、填空题（本大题共5小题，共15.0分）

11. 任意写出 $- 2$ 到 $- 1$ 之间一个无理数．

查看试题解析
12. 若两个连续整数x、y满足x＜ $\sqrt{5}$ +1＜y，则x+y的值是．

查看试题解析
13. 计算： $2015 \times 2017 - 201 6^{2} =$ ．

查看试题解析
14. 若 $| a + 2 | + a^{2} - 4 a b + 4 b^{2} = 0$ ，则 $a =$ ， $b =$ ．

查看试题解析
15. 观察下列等式：
$(x - 1) (x + 1) = x^{2} - 1$ ；
$(x - 1) (x^{2} + x + 1) = x^{3} - 1$ ；
$(x - 1) (x^{3} + x^{2} + x + 1) = x^{4} - 1$ ；
$\dots$ ；
利用你发现的规律回答：若 $(x - 1) (x^{6} + x^{5} + x^{4} + x^{3} + x^{2} + x + 1) = - 2$ ，则 $x^{2016}$ 的值是．

查看试题解析

三、解答题（本大题共8小题，共75.0分。解答应写出文字说明，证明过程或演算步骤）

16. 计算：

(1)、 $\sqrt{16} - \sqrt[3]{- 8} + \sqrt[3]{- \frac{1}{27}}$ ；

(2)、 $\sqrt{9} + \sqrt[3]{- 125} + | \sqrt{3} - 2 |$ ．

查看试题解析
17. 若实数 $b$ 的两个不同平方根是 $2 a - 3$ 和 $3 a - 7$ ，求 $5 a - b$ 的平方根．

查看试题解析
18. 运用公式进行简便计算：

(1)、 $20 \frac{2}{3} \times 19 \frac{1}{3}$ ；

(2)、 $49 9^{2}$ ．

查看试题解析
19. 先化简，再求值：

(1)、 $(x + 5) (x - 1) + (x - 2)^{2}$ ，其中 $x = - 2$ ；

(2)、已知 $3 a^{2} - 4 a - 7 = 0$ ，求代数式 $(2 a - 1)^{2} - (a + b) (a - b) - b^{2}$ 的值．

查看试题解析
20. 如图①是由8个同样大小的立方体组成的魔方，体积为8.

(1)、求出这个魔方的棱长；

(2)、图①中阴影部分是一个正方形 $A B C D$ ，求出阴影部分的面积及其边长.

(3)、把正方形 $A B C D$ 放到数轴上，如图②，使得点 $A$ 与 $- 1$ 重合，那么点 $D$ 在数轴上表示的数为.

查看试题解析
21. 数学老师在课堂上提出一个问题：“通过探究知道： $\sqrt{2} \approx 1.414 \dots$ ，它是个无限不循环小数，也叫无理数，它的整数部分是 $1$ ，那么有谁能说出它的小数部分是多少？”，小明举手回答：它的小数部分我们无法全部写出来，但可以用 $\sqrt{2} - 1$ 来表示它的小数部分，张老师夸奖小明真聪明，肯定了他的说法 $.$ 现请你根据小明的说法解答：

(1)、 $\sqrt{5}$ 的小数部分是 $a$ ， $\sqrt{13}$ 的整数部分是 $b$ ，求 $a + b - \sqrt{5}$ 的值．

(2)、已知 $8 + \sqrt{3} = x + y$ ，其中 $x$ 是一个整数， $0 < y < 1$ ，求 $3 x + (y - \sqrt{3})^{2018}$ 的值．

查看试题解析
22. 我们知道，对于一个图形，通过两种不同的方法计算它的面积，可以得到一个数学等式 $.$ 例如由图 $1$ 可以得到 $(a + 2 b) (a + b) = a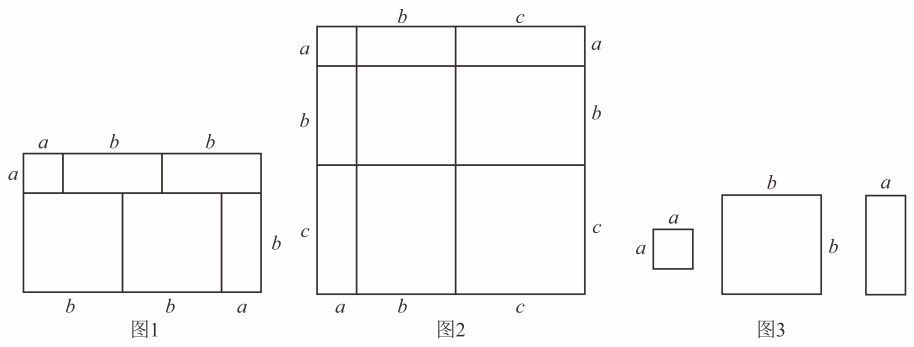^{2} + 3 a b + 2 b^{2}$ ，请回答下列问题：

(1)、写出图 $2$ 中所表示的数学等式：；

(2)、利用 $(1)$ 中所得的结论，解决下列问题：已知 $a + b + c = 11$ ， $a b + b c + a c = 38$ ，求 $a^{2} + b^{2} + c^{2}$ 的值；

(3)、图 $3$ 中给出了若干个边长为 $a$ 和边长为 $b$ 的小正方形纸片及若干个长为b 、宽为 $a$ 的长方形纸片 $.$ 请按要求利用所给的纸片拼出一个几何图形，并画在所给的方框内，要求所拼的几何图形的面积为： $2 a^{2} + 5 a b + 2 b^{2}$ ．

查看试题解析
23. 【阅读理解】“若 $x$ 满足 $(7 - x) (x - 3) = 3$ ，求 ${(7 - x)}^{2} + {(x - 3)}^{2}$ 的值”．
解：设 $7 - x = a$ ， $x - 3 = b$ ，则 $(7 - x) (x - 3) = a b = 3$ ， $a + b = (7 - x) + (x - 3) = 4$ ， $(7 - x)^{2} + (x - 3)^{2} = a^{2} + b^{2} = (a + b)^{2} - 2 a b = 4^{2} - 2 \times 3 = 10$ ．
【解决问题】

(1)、若 $x$ 满足 $(4 - x) (x - 3) = - 2$ ，则 ${(4 - x)}^{2} + {(x - 3)}^{2}$ 的值为；

(2)、若 $x$ 满足 $(2 x + 3) (2 x - 1) = \frac{9}{2}$ ，则 $(2 x + 3)^{2} + (2 x - 1)^{2}$ 的值为；

(3)、如图，点 $C$ 是线段 $A B$ 上的一点，以 $A C$ ， $B C$ 为边向两边作正方形，设 $A B = 5$ ，两正方形的面积和 $S_{1} + S_{2} = 13$ ，求图中阴影部分面积．

查看试题解析