北师大版数学八年级（上）复习微专题精炼4 实数及运算

试卷更新日期：2023-10-24 类型：复习试卷

进入出卷网下载

一、选择题

1. 下列各数： $\sqrt{9} ， \frac{22}{7} ， π ， \sqrt[3]{2} ， - 1.34$ ，其中，无理数的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列说法正确的是（　　）

A、 $\sqrt{16}$ 的平方根是 $\pm 4$ B、无限小数是无理数 C、数轴上的点对应的数不是整数就是分数 D、若a ， b ， c为一组勾股数，则2a ， 2b ， 2c仍是一组勾股数

查看试题解析
3. 一个数的两个平方根分别是2a+1与-3a+2，则a的值是（）

A、-1 B、1 C、-3 D、3

查看试题解析
4. 已知 $\sqrt{12 + m}$ 是整数，则自然数 $m$ 的最小值是（）

A、 $2$ B、 $4$ C、 $8$ D、 $11$

查看试题解析
5. 下列运算结果错误的是（）

A、 $\sqrt{(- 2)^{2}} = 2$ B、 $(- \sqrt{2})^{2} = 2$ C、 $\sqrt{4} = \pm 2$ D、 $\sqrt[3]{- 8} = - 2$

查看试题解析
6. 已知 $x$ 没有平方根，且 $| x | = 125$ ，则 $x$ 的立方根为（）

A、 $25$ B、 $- 25$ C、 $\pm 5$ D、 $- 5$

查看试题解析
7. 已知 $x$ ， $y$ 为实数，且 $\sqrt{x - 3} + (y + 2)^{2} = 0$ ，则 $y^{x}$ 的立方根是（）

A、 $\sqrt[3]{6}$ B、 $- 8$ C、 $- 2$ D、 $\pm 2$

查看试题解析
8. 下列说法正确的有（）
①带根号的数都是无理数；

②立方根等于本身的数是0和1；

③-a一定没有平方根；

④实数与数轴上的点是一一对应的；

⑤两个无理数的差还是无理数．

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 为了证明数轴上的点可以表示无理数，老师给学生设计了如下材料：如图，直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上一点由原点（记为点O）到达点A ，点A对应的数是（　　）

A、 $π$ B、3.14 C、 $- π$ D、-3.14

查看试题解析
10. 公元前500年，毕达哥拉斯学派中的一名成员西伯索斯发现了无理数，导致了第一次数学危机．事实上，我国古代发现并阐述无理数的概念比西方更早，但是没有系统的理论．《九章算术》的开方术中指出了存在有开不尽的情形：“若开方不尽者，为不可开．”《九章算术》的作者们给这种“不尽根数”起了一个专门名词—“面”“面”就是无理数．无理数中最具有代表性的数就是“ $\sqrt{2}$ ”．下列关于 $\sqrt{2}$ 的说法错误的是（）

A、可以在数轴上找到唯一一点与之对应 B、它是面积为2的正方形的边长 C、可以用两个整数的比表示 D、可以用反证法证明它不是有理数

查看试题解析

二、填空题

11. 已知m，n为两个连续整数，且 $m < \sqrt{13} < n$ ，则 $m + n =$ ．

查看试题解析
12. 阅读下列材料：因为 $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ，即 $2 < \sqrt{5} < 3$ ，所以 $\sqrt{5}$ 的整数部分为 $2$ ，小数部分为 $\sqrt{5} - 2$ ，若规定实数 $m$ 的整数部分记为 $[m]$ ，小数部分记为 ${m}$ ，可得 $[\sqrt{5}] = 2$ ， ${\sqrt{5}} = \sqrt{5} - 2 .$ 按照此规定计 ${5 - \sqrt{5}}$ 的值是．

查看试题解析
13. 已知：y= $\sqrt{a - 2} + \sqrt{3 (b + 1)}$ ，当a，b取不同的值时，y也有不同的值，当y最小时，b^a的算术平方根为.

查看试题解析
14. 计算 $\sqrt[3]{- \frac{8}{27}}$ 的结果等于.

查看试题解析
15. 如图，由图中的信息可知点P表示的数是.

查看试题解析

三、计算题

16. 计算：

(1)、 $(1 + \sqrt{3}) (2 - \sqrt{3})$

(2)、 $\frac{\sqrt{36} \times \sqrt{12}}{\sqrt{3}}$

(3)、 $\sqrt{18} - \sqrt{8} + \sqrt{\frac{1}{8}}$

(4)、 $（ 3 \sqrt{18} + \frac{1}{5} \sqrt{50} - 4 \sqrt{\frac{1}{2}} ） \div \sqrt{32}$

查看试题解析

四、解答题

17. 解下列各题：

(1)、计算： $\sqrt[3]{- 27} + \sqrt{5} (\sqrt{5} - \frac{1}{\sqrt{5}})$ ；

(2)、计算： $| \sqrt{3} | + {(\sqrt{3} - \frac{1}{2})}^{2} - {(\sqrt{3} + \frac{1}{2})}^{2}$ ；

(3)、如图，点A是数轴上表示实数a的点．

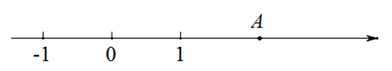
①用直尺和圆规在数轴上作出表示实数的 $\sqrt{2}$ 的点P；（保留作图痕迹，不写作法）

②利用数轴比较 $\sqrt{2}$ 和a的大小，并说明理由．

查看试题解析
18. 已知 $a - 4$ 的立方根是 $1$ ， $3 a - b - 2$ 的算术平方根是 $3$ ， $\sqrt{13}$ 的整数部分是 $c$ ．

(1)、求 $a$ ， $b$ ， $c$ 的值．

(2)、求 $2 a - 3 b + c$ 的平方根．

查看试题解析
19. 一只蚂蚁从点A沿数轴向左爬了2个单位长度到达点B ，点A表示 $\sqrt{3}$ ，设点B所表示的数为m ．

(1)、求 $| m + 1 | + | m - 1 |$ 的值．

(2)、在数轴上还有C、D两点分别表示实数C、d ，且满足 $\sqrt{c + 3} + | d - 9 | = 0$ ，求cd的立方根．

查看试题解析
20. 阅读下面的文字，解答问题．
例如：∵ $\sqrt{4} < \sqrt{7} < \sqrt{9}$ ，即 $2 < \sqrt{7} < 3$ ，
∴ $\sqrt{7}$ 的整数部分为2，小数部分为 $\sqrt{7} - 2$ ，
请解答：

(1)、 $\sqrt{15}$ 的整数部分是；

(2)、已知： $8 - \sqrt{15}$ 小数部分是 $m$ ， $8 + \sqrt{15}$ 小数部分是 $n$ ，且 ${(x - 1)}^{2} - m = n$ ，求 $x$ 的值．

查看试题解析
21. 新定义：若无理数 $\sqrt{T}$ 的被开方数 $T$ （ $T$ 为正整数）满足 $n^{2} < T < (n + 1)^{2}$ （其中 $n$ 为正整数），则称无理数 $\sqrt{T}$ 的“青一区间”为 $(n ， n + 1)$ ；同理规定无理数 $- \sqrt{T}$ 的“青一区间”为 $(- n - 1 ， - n)$ ．例如：因为 $1^{2} < 2 < 2^{2}$ ，所以 $1 < \sqrt{2} < 2$ ，所以 $\sqrt{2}$ 的“青一区间”为 $(1 ， 2)$ ， $- \sqrt{2}$ 的“青一区间”为 $(- 2 ， - 1)$ ．请解答下列问题：

(1)、 $\sqrt{17}$ 的“青一区间”是； $- \sqrt{23}$ 的“青一区间”是；

(2)、若无理数 $- \sqrt{a}$ （ $a$ 为正整数）的“青一区间”为 $(- 3 ， - 2)$ ， $\sqrt{a + 3}$ 的“青一区间”为 $(3 ， 4)$ ，求 $\sqrt[3]{a + 1}$ 的值；

(3)、实数x ， y ， m满足关系式： $\sqrt{2 x + 3 y - m} + \sqrt{3 x + 4 y - 2 m} = \sqrt{x + y - 2023} + \sqrt{2023 - x - y}$ ，求 $m$ 的算术平方根的“青一区间”．

查看试题解析