北师大版数学八年级（上）复习微专题精炼3 勾股定理的应用

试卷更新日期：2023-10-24 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图，一根长为 $5 m$ 的竹竿 $A B$ 斜靠在竖直的墙壁上，竹竿底端B离墙壁距离 $3 m$ ，则该竹竿的顶端A离地竖直高度为（）

A、 $2 m$ B、 $3 m$ C、 $4 m$ D、 $\sqrt{3} m$

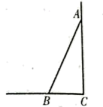查看试题解析
2. 如图，在“庆国庆，手拉手”活动中，某小组从营地A出发，沿北偏东 $53 °$ 方向走了1200m到达B点，然后再沿北偏西 $37 °$ 方向走了500m到达目的地C点，此时A，C两点之间的距离为（）

A、1000m B、1100m C、1200m D、1300m

查看试题解析
3. 《九章算术》中记录了这样一则“折竹抵地”问题：今有竹高一丈，末折抵地，去本四尺，问折者高几何？意思是：一根竹子，原高一丈，一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部4尺远（如图），则折断后的竹子高度为多少尺？（1丈=10尺）如果我们假设折断后的竹子高度为 $x$ 尺，根据题意，可列方程为（　　）

A、 $x^{2} + 4^{2} = 1 0^{2}$ B、 ${(10 - x)}^{2} + 4^{2} = 1 0^{2}$ C、 ${(10 - x)}^{2} + 4^{2} = x^{2}$ D、 $x^{2} + 4^{2} = {(10 - x)}^{2}$

查看试题解析
4. 如图，将一根长 $20 c m$ 的铅笔放入底面直径为 $9 c m$ ，高为 $12 c m$ 的圆柱形笔筒中，设铅笔露在笔筒外面的长度为 $x c m$ ，则x的最小值是（）

A、5 B、7 C、12 D、13

查看试题解析
5. 如图，长方体的高为 $9 d m$ ，底面是边长为 $6 d m$ 的正方形 $.$ 一只蚂蚁从顶点 $A$ 开始爬向顶点 $B$ ，那么它爬行的最短路程为（）

A、 $10 d m$ B、 $12 d m$ C、 $15 d m$ D、 $20 d m$

查看试题解析
6. 如图，某超市为了吸引顾客，在超市门口离地高4.5m的墙上，装有一个由传感器控制的门铃A，如①图所示，人只要移至该门铃5m及5m以内时，门铃就会自动发出语音“欢迎光临”.如②图所示，一个身高1.5m的学生走到D处，门铃恰好自动响起，则BD的长为（）

A、3米 B、4米 C、5米 D、7米

查看试题解析
7. 有长为5cm，12cm的两根木条，现想找一根木条和这两根木条首尾顺次相连组成直角三角形，则下列木条长度适合的是（）

A、10cm B、13cm C、18cm D、20cm

查看试题解析
8. 汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝．如图所示的弦图中，四个直角三角形都是全等的，它们的斜边长为5，较短直角边长为3，则图中小正方形（空白区域）的面积为（）

A、1 B、4 C、6 D、9

查看试题解析
9. 勾股定理是人类早期发现并证明的重要数学定理之一，是用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一．它不但因证明方法层出不穷吸引着人们，更因为应用广泛而使人入迷．如图，秋千静止时，踏板离地的垂直高度 $B E = 1 m$ ，将它往前推 $6 m$ 至 $C$ 处时（即水平距离 $C D = 6 m$ ），踏板离地的垂直高度 $C F = 4 m$ ，它的绳索始终拉直，则绳索 $A C$ 的长是（） $m$

A、 $\frac{21}{2}$ B、 $\frac{15}{2}$ C、6 D、 $\frac{9}{2}$

查看试题解析
10. 有一个边长为1的正方形，以它的一条边为斜边，向外作一个直角三角形，再分别以直角三角形的两条直角边为边，向外各作一个正方形，称为第一次“生长”（如图1）；再分别以这两个正方形的边为斜边，向外各自作一个直角三角形，然后分别以这两个直角三角形的直角边为边，向外各作一个正方形，称为第二次“生长”（如图2）……如果继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是（）

A、1 B、2020 C、2021 D、2022

查看试题解析

二、填空题

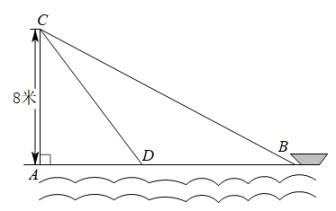
11. 《九章算术》是古代东方数学代表作，汇集了我国历代学者的劳动和智慧，被誉为人类科学史上应用数学的“算经之首”．其中记录了这样一个问题，原文：今有竹高一丈，末折抵地，去本三尺．问折者高几何？意思是：今有竹高10尺，末端被折断而抵达地面，离竹根部有3尺，则竹的余高为尺．

查看试题解析
12. 如图，在离水面高度为8米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为17米，几分钟后船到达点D的位置，此时绳子CD的长为10米，问船向岸边移动了米.

查看试题解析
13. 在平静的湖面上，有一朵荷花高出水面半尺，忽然一阵强风吹来把荷花垂直拉到水里且荷花恰好落在水面．花在水平方向上离开原来的位置2尺远，则这个湖的水深是尺．

查看试题解析
14. 一轮船以16海里/时的速度从A港向东北方向航行，另一艘船同时以12海里/时的速度从A港向西北方向航行，经过 $1.5$ 小时后，它们相距海里．

查看试题解析
15. 我国古代《九章算术》中的“折竹抵地问题”：一根竹子高一丈，折断后竹子顶端落在离竹子底端6尺处，折断处离地面的高度为尺．（一丈=10尺）

查看试题解析

三、解答题

16. 如图所示，某住宅社区在相邻两楼之间修建一个上方是一个半圆，下方是长方形的仿古通道，现有一辆卡车装满家具后，高4米，宽2.8米，求这辆送家具的卡车能否通过这个通道.

查看试题解析
17. 学过 $《$ 勾股定理 $》$ 后，某班兴趣小组来到操场上测量旗杆 $A B$ 的高度，得到如下信息：

①测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长 $2$ 米 $($ 如图 $1)$ ；
②当将绳子拉直时，测得此时拉绳子另一端的手到地面的距离 $C D$ 为 $2$ 米，到旗杆的距离 $C E$ 为 $10$ 米 $($ 如图 $2)$ ．根据以上信息，求旗杆 $A B$ 的高度．

查看试题解析

四、综合题

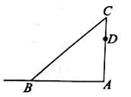
18. 如图，一根直立的旗杆高8m，因刮大风旗杆从点C处折断，顶部B着地且离旗杆底部A的距离为4m．

(1)、求旗杆距地面多高处折断（ $A C$ ）；

(2)、工人在修复的过程中，发现在折断点C的下方1m的点D处，有一条明显裂痕，将旗杆修复后，若下次大风将旗杆从点D处吹断，则距离旗杆底部周围多大范围内有被砸伤的风险？

查看试题解析
19. 台风是一种自然灾害，它在以台风中心为圆心，一定长度为半径的圆形区域内形成极端气候，有极强的破坏力．如图，监测中心监测到一台风中心沿监测点B与监测点A所在的直线由东向西移动，已知点C为一海港，且点C与A，B两点的距离分别为300km、400km，且 $∠ A C B = 90 °$ ，过点 $C$ 作 $C E ⊥ A B$ 于点 $E$ ，以台风中心为圆心，半径为260km的圆形区域内为受影响区域，台风的速度为25km/h．

(1)、求监测点A与监测点B之间的距离；

(2)、请判断海港C是否会受此次台风的影响，若受影响，则台风影响该海港多长时间？若不受影响，请说明理由．

查看试题解析
20. 在一条东西走向的河的一侧有一村庄C，河边原有两个取水点A，B，其中 $A B = A C$ ，由于某种原由C到A的路现在已经不通，某村为方便村民取水决定在河边新建一个取水点H（A、H、B在一条直线上），并新修一条路CH，测得 $C B = 1.5$ 千米， $C H = 1.2$ 千米， $H B = 0.9$ 千米．

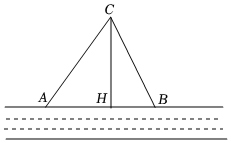(1)、问CH是否为从村庄C到河边的最近路？请通过计算加以说明．

(2)、求原来的路线AC的长．

查看试题解析