北师大版数学八年级(上)复习微专题精炼2 勾股定理的逆定理
试卷更新日期:2023-10-24 类型:复习试卷
一、选择题
-
1. 在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中错误的是( )A、如果a2=b2−c2 , 那么△ABC是直角三角形且∠A=90° B、如果∠A:∠B:∠C=1:2:3,那么△ABC是直角三角形 C、如果 , 那么△ABC是直角三角形 D、如果 , 那么△ABC是直角三角形2. 在下列条件中:①;②;③;④ , 能确定是直角三角形的条件有( )A、1个 B、2个 C、3个 D、4个3. 在中,的对边分别是a,b,c,下列条件中不能说明 是直角三角形是( )A、 B、 C、 D、4. 将直角三角形的三条边长做如下变化,得到的新三角形仍是直角三角形的是( )A、同加一个相同的数 B、同减一个相同的数 C、同乘以一个相同的正整数 D、同时平方5. 在 中,的对边分别为 , 下列所给数据中, 能判断是直角三角形的是( )A、 B、 C、 D、6. 如图,在边长为1的正方形方格中,A,B,C,D均为格点,构成图中三条线段 , , .现在取出这三条线段 , , 首尾相连拼三角形.下列判断正确的是( )
 A、能拼成一个锐角三角形 B、能拼成一个直角三角形 C、能拼成一个钝角三角形 D、不能拼成三角形7. 在△ABC中,它的三边分别为a,b,c,条件:①∠A=∠C-∠B;②∠A=∠B=2∠C;③∠A:∠B:∠C=3:4:5;④a:b:c=1::;中,能确定△ABC是直角三角形的条件有( )A、1个 B、2个 C、3个 D、4个8. 如图折叠直角三角形纸片 , 使直角边落在斜边上折痕为 , 点落到点处 , 已知 , , , 则的长是( )
A、能拼成一个锐角三角形 B、能拼成一个直角三角形 C、能拼成一个钝角三角形 D、不能拼成三角形7. 在△ABC中,它的三边分别为a,b,c,条件:①∠A=∠C-∠B;②∠A=∠B=2∠C;③∠A:∠B:∠C=3:4:5;④a:b:c=1::;中,能确定△ABC是直角三角形的条件有( )A、1个 B、2个 C、3个 D、4个8. 如图折叠直角三角形纸片 , 使直角边落在斜边上折痕为 , 点落到点处 , 已知 , , , 则的长是( ) A、3 B、4 C、5 D、69. 如图,在4个均由16个小正方形组成的网格正方形中,各有一个格点三角形,那么这4个正方形网格中不是直角三角形的是( )A、
A、3 B、4 C、5 D、69. 如图,在4个均由16个小正方形组成的网格正方形中,各有一个格点三角形,那么这4个正方形网格中不是直角三角形的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,五根小木棒,其长度分别为5,9,12,13,15,现将它们摆成两个直角三角形,其中正确的是( )A、
10. 如图,五根小木棒,其长度分别为5,9,12,13,15,现将它们摆成两个直角三角形,其中正确的是( )A、 B、
B、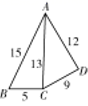 C、
C、 D、
D、
二、填空题
-
11. 已知一个三角形的三边长分别是4cm、7cm、6cm,该三角形的形状(填“是”或“不是”)直角三角形.12. 如图,每个小正方形的边长为1,则∠ABC的度数为度.
 13. 下列条件:①∠C=∠A-∠B;②∠A:∠B:∠C=5∶2∶3;③a=c,b=c;④a∶b∶c=1∶2: , 则能确定△ABC是直角三角形的条件有个.14. 三角形的三边长a,b,c满足2ab=(a+b)2-c2 , 则此三角形的形状是三角形.15. 定义:在平面直角坐标系中,把从点P出发沿横或纵方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若 , ,则P,Q的“实际距离”为5,即 或 .环保低碳的公共自行车,逐渐成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为 , , ,若点M表示公共自行车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标是.
13. 下列条件:①∠C=∠A-∠B;②∠A:∠B:∠C=5∶2∶3;③a=c,b=c;④a∶b∶c=1∶2: , 则能确定△ABC是直角三角形的条件有个.14. 三角形的三边长a,b,c满足2ab=(a+b)2-c2 , 则此三角形的形状是三角形.15. 定义:在平面直角坐标系中,把从点P出发沿横或纵方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若 , ,则P,Q的“实际距离”为5,即 或 .环保低碳的公共自行车,逐渐成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为 , , ,若点M表示公共自行车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标是.
三、作图题
-
16. 如图是5×5的网格,每个小正方形的边长均为1,分别在图1、图2中各画一个以AB为斜边的的直角三角形.(要求:所画三角形顶点都在格点上 , 两个三角形面积不同).

四、解答题
-
17. 已知的三条边长分别为 , , , 其中 , , , 且是直角三角形吗?请证明你的判断.18. 为庆祝中华人民共和国成立73周年,喜迎党的二十大胜利召开,学校组织了“献礼二十大”小制作展示活动.小彬计划制作一架飞机模型,如图的四边形材料是飞机垂直尾翼的雏形.小彬测量发现 , , , . 根据设计要求,还需保证 . 由于手头工具有限,小彬只能测得 . 根据以上数据,请你判断该材料是否符合设计要求,并说明理由.

五、综合题
-
19. 如图,网格中每个小正方形的边长都是1,点A、B、C、D都在格点上.
 (1)、线段AB的长度是 , 线段CD的长度是 .(2)、若EF的长为 , 那么以AB、CD、EF三条线段为边能否构成直角三角形,并说明理由.
(1)、线段AB的长度是 , 线段CD的长度是 .(2)、若EF的长为 , 那么以AB、CD、EF三条线段为边能否构成直角三角形,并说明理由.
-