北师大版数学八年级(上)复习微专题精炼1 勾股定理
试卷更新日期:2023-10-24 类型:复习试卷
一、选择题
-
1. 在中, , , , 则BC的长为( )A、6 B、8 C、10 D、122. 已知直角三角形的斜边长为10,两直角边的比为3∶4,则较短直角边的长为( )A、3 B、6 C、8 D、53. 已知直角三角形两边的长分别为和 , 则此三角形的周长为( )A、 B、 C、或 D、4. 如图在一个高为米,长为米的楼梯表面铺地毯,则地毯至少需要( )
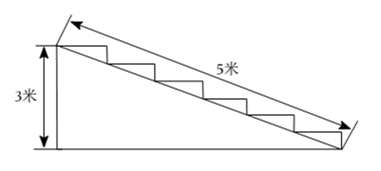 A、米 B、米 C、米 D、米5. 如图,在2×2的正方形网格中,每个小正方形边长为1,点A,B,C均为格点,以点A为圆心,AB长为半径作弧,交格线于点D,则CD的长为( )
A、米 B、米 C、米 D、米5. 如图,在2×2的正方形网格中,每个小正方形边长为1,点A,B,C均为格点,以点A为圆心,AB长为半径作弧,交格线于点D,则CD的长为( )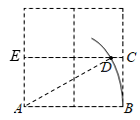 A、 B、 C、 D、6. 如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,大正方形面积为S1 , 小正方形面积为S2 , 则(a+b)2可表示为( )
A、 B、 C、 D、6. 如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,较短直角边长为b,大正方形面积为S1 , 小正方形面积为S2 , 则(a+b)2可表示为( ) A、S1-S2 B、2S1-S2 C、S1+S2 D、S1+2S27. 将一个等腰三角形纸板沿垂线段 , 进行剪切,得到三角形 , 再按如图2方式拼放,其中与共线.若 , 则的长为( )
A、S1-S2 B、2S1-S2 C、S1+S2 D、S1+2S27. 将一个等腰三角形纸板沿垂线段 , 进行剪切,得到三角形 , 再按如图2方式拼放,其中与共线.若 , 则的长为( ) A、 B、 C、 D、78. 如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形ABCD的四条边为边向外作四个正方形,面积分别为S1 , S2 , S3 , S4 . 若S1=48,S2+S3=135,则S4=( )
A、 B、 C、 D、78. 如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形ABCD的四条边为边向外作四个正方形,面积分别为S1 , S2 , S3 , S4 . 若S1=48,S2+S3=135,则S4=( )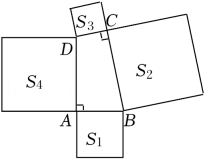 A、183 B、87 C、119 D、819. 如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D'处,若AB=3,AD=4,则ED的长为( )
A、183 B、87 C、119 D、819. 如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D'处,若AB=3,AD=4,则ED的长为( ) A、 B、3 C、1 D、10. 已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A、 B、3 C、1 D、10. 已知,如图长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图,四边形ABCD , 连接BD , AB⊥AD , CE⊥BD , AB=CE , BD=CD . 若AD=5,CD=7,则BE= .
 12. 已知如图:小正方形边长为 , 连接小正方形的三个顶点,可得 , 则的周长为 .
12. 已知如图:小正方形边长为 , 连接小正方形的三个顶点,可得 , 则的周长为 . 13. 在Rt△ABC中,∠B=90°,AB=4,BC=8,D、E分别是边AC、BC上的点,将△ABC沿着DE进行翻折,点A和点C重合,则EC=.
13. 在Rt△ABC中,∠B=90°,AB=4,BC=8,D、E分别是边AC、BC上的点,将△ABC沿着DE进行翻折,点A和点C重合,则EC=. 14. 如图,在 中, , 是 边上除 , 点外的任意一点,则 .
14. 如图,在 中, , 是 边上除 , 点外的任意一点,则 . 15. 阅读材料:在直角三角形中,斜边和两条直角边满足定理:两条直角边的平方和,等于斜边的平方,因此如果已知两条边的长,根据定理就能求出第三边的长,例如:在中,已知 , , , 由定理得 , 代入数据计算求得 .
15. 阅读材料:在直角三角形中,斜边和两条直角边满足定理:两条直角边的平方和,等于斜边的平方,因此如果已知两条边的长,根据定理就能求出第三边的长,例如:在中,已知 , , , 由定理得 , 代入数据计算求得 .请结合上述材料和已学几何知识解答以下问题:
已知:如图, , , , , , 点是的中点,那么的长为 .

三、解答题
-
16. 如图,中, , , AD平分∠BAC交BC于点D,分别以点A和点C为圆心,大于的长为半径作弧,两弧相交于点M和点N,连接MN,交AD于点E,求AE的长.
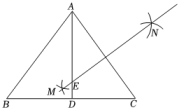 17. 如图,在四边形中, ,E为 上一点.将四边形沿折叠,使点重合,求折痕的长.
17. 如图,在四边形中, ,E为 上一点.将四边形沿折叠,使点重合,求折痕的长. 18. 如图,在长方形中, , E为上一点,把沿折叠,使点C落在边上的F处.
18. 如图,在长方形中, , E为上一点,把沿折叠,使点C落在边上的F处.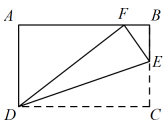 (1)、求的长;(2)、求的长.19. 如图1,将射线按逆时针方向旋转β角,得到射线 , 如果点P为射线上的一点,且 , 那么我们规定用表示点P在平面内的位置,并记为 , 例如,图2中,如果 , , 那么点M在平面内的位置,记为 , 根据图形,解答下面的问题:
(1)、求的长;(2)、求的长.19. 如图1,将射线按逆时针方向旋转β角,得到射线 , 如果点P为射线上的一点,且 , 那么我们规定用表示点P在平面内的位置,并记为 , 例如,图2中,如果 , , 那么点M在平面内的位置,记为 , 根据图形,解答下面的问题: (1)、如图3,如果点N在平面内的位置记为 , 那么; .(2)、如果点A、B在平面内的位置分别记为 , 试求A、B两点之间的距离并画出图.20. 为了探索代数式的最小值,
(1)、如图3,如果点N在平面内的位置记为 , 那么; .(2)、如果点A、B在平面内的位置分别记为 , 试求A、B两点之间的距离并画出图.20. 为了探索代数式的最小值,小张巧妙的运用了数学思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作 , 连结AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则 , 则问题即转化成求AC+CE的最小值.
 (1)、我们知道当A、C、E在同一直线上时,AC+CE的值最小,于是可求得的最小值等于 , 此时x=;(2)、题中“小张巧妙的运用了数学思想”是指哪种主要的数学思想;
(1)、我们知道当A、C、E在同一直线上时,AC+CE的值最小,于是可求得的最小值等于 , 此时x=;(2)、题中“小张巧妙的运用了数学思想”是指哪种主要的数学思想;(选填:函数思想,分类讨论思想、类比思想、数形结合思想)
(3)、请你根据上述的方法和结论,试构图求出代数式的最小值.