【每日15min】26扇形面积的计算—浙教版数学九(上)微专题精炼
试卷更新日期:2023-10-23 类型:复习试卷
一、选择题
-
1. 如图,点A , B , C在上, , 连接 , . 若的半径为3,则扇形(阴影部分)的面积为( )
 A、 B、 C、 D、2. 已知一个扇形的面积是 , 弧长是 , 则这个扇形的半径为( )A、24 B、22 C、12 D、63. 如图,正五边形内接于 , 其半径为 , 作交于点 , 则图中影部分的面积为( )
A、 B、 C、 D、2. 已知一个扇形的面积是 , 弧长是 , 则这个扇形的半径为( )A、24 B、22 C、12 D、63. 如图,正五边形内接于 , 其半径为 , 作交于点 , 则图中影部分的面积为( ) A、 B、 C、 D、4. 如果用定长为的线段围成一个扇形,且使得这个扇形的面积最大,方法应为( )A、使扇形所在圆的半径等于 B、使扇形所在圆的半径等于 C、使扇形的圆心角为 D、使扇形的圆心角为5. 如图,某小区要绿化一扇形空地,准备在小扇形内种花在其余区域内(阴影部分)种草,测得 , , , 则种草区域的面积为( )
A、 B、 C、 D、4. 如果用定长为的线段围成一个扇形,且使得这个扇形的面积最大,方法应为( )A、使扇形所在圆的半径等于 B、使扇形所在圆的半径等于 C、使扇形的圆心角为 D、使扇形的圆心角为5. 如图,某小区要绿化一扇形空地,准备在小扇形内种花在其余区域内(阴影部分)种草,测得 , , , 则种草区域的面积为( ) A、 B、 C、 D、6. 如图,是的外接圆,半径为4,连接OB,OC,OA,若 , , 则阴影部分的面积是( )
A、 B、 C、 D、6. 如图,是的外接圆,半径为4,连接OB,OC,OA,若 , , 则阴影部分的面积是( ) A、 B、 C、 D、7. 如图,是的直径,弦与垂直,垂足为点E,连接并延长交于点 , , , 则图中阴影部分的面积为( )
A、 B、 C、 D、7. 如图,是的直径,弦与垂直,垂足为点E,连接并延长交于点 , , , 则图中阴影部分的面积为( ) A、 B、 C、 D、8. 如图,在中, , , 则图中阴影部分的面积为( )
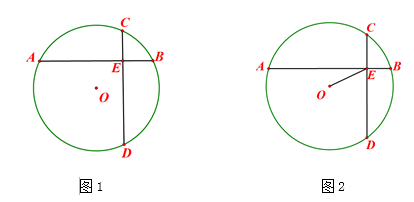
A、 B、 C、 D、8. 如图,在中, , , 则图中阴影部分的面积为( ) A、 B、 C、 D、9. 如果一个扇形的圆心角扩大为原来的2倍,半径扩大为原来的3倍,那么这个扇形的面积将扩大为原来的倍数是( )A、18 B、12 C、6 D、410. 【阅读理解】在求阴影部分面积时,常常会把原图形的一部分割下来补在图形中的另一部分,使其成为基本规则图形,从而使问题得到解决,这种方法称为割补法.如图1,C是半圆O的中点,欲求阴影部分面积,只需把弓形BC割下来,补在弓形处,则 .
A、 B、 C、 D、9. 如果一个扇形的圆心角扩大为原来的2倍,半径扩大为原来的3倍,那么这个扇形的面积将扩大为原来的倍数是( )A、18 B、12 C、6 D、410. 【阅读理解】在求阴影部分面积时,常常会把原图形的一部分割下来补在图形中的另一部分,使其成为基本规则图形,从而使问题得到解决,这种方法称为割补法.如图1,C是半圆O的中点,欲求阴影部分面积,只需把弓形BC割下来,补在弓形处,则 .
【拓展应用】如图2,以为直径作半圆O,C为的中点,连接 , 以为直径作半圆P,交于点D.若 , 则图中阴影部分的面积为( )
A、 B、 C、 D、二、填空题
-
11. 如图,中 , , 将绕点逆时针旋转得到当点恰好落在斜边上时图中阴影部分的面积为 .
 12. 如图,已知正六边形内接于半径为2的 , 点 , 分别是 , 的中点,连结 , , , , , , 则图中阴影部分的面积为.
12. 如图,已知正六边形内接于半径为2的 , 点 , 分别是 , 的中点,连结 , , , , , , 则图中阴影部分的面积为. 13. 在2×2的正方形网格中,每个小正方形的边长为1.以点O为圆心,2为半径画弧,交图中网格线于点A,B,则扇形AOB的面积是.
13. 在2×2的正方形网格中,每个小正方形的边长为1.以点O为圆心,2为半径画弧,交图中网格线于点A,B,则扇形AOB的面积是.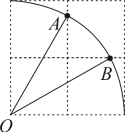 14. 三个正方形方格和扇形的位置如图所示,点O为扇形的圆心,格点A,B,C分别在扇形的两条半径和弧上,已知每个方格的边长为1,则扇形的面积为 .
14. 三个正方形方格和扇形的位置如图所示,点O为扇形的圆心,格点A,B,C分别在扇形的两条半径和弧上,已知每个方格的边长为1,则扇形的面积为 .
三、解答题
-
15. 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上.
 (1)、画出△ABC绕C点顺时针旋转90°得到的△A1B1C , 直接写出A1的坐标为 ▲ ;(2)、若△A2B2C2和△ABC , 关于原点O成中心对称,请画出△A2B2C2;(3)、在(1)的旋转过程中,求CA扫过图形的面积.
(1)、画出△ABC绕C点顺时针旋转90°得到的△A1B1C , 直接写出A1的坐标为 ▲ ;(2)、若△A2B2C2和△ABC , 关于原点O成中心对称,请画出△A2B2C2;(3)、在(1)的旋转过程中,求CA扫过图形的面积.