【每日15min】25弧长的计算—浙教版数学九(上)微专题精炼
试卷更新日期:2023-10-23 类型:复习试卷
一、选择题
-
1. 如图,在3×3方格中(每个小方格的边长为1个单位),点A、B、O都在格点上,以O为圆心,OA为半径作弧,交OB于点C,则的长为( )
 A、π B、π C、π D、π2. 如图,在Rt△ABC中,∠A=20°,AC=6,将△ABC绕直角顶点C按顺时针方向旋转得到△A′B′C,当点B′第一次落在AB边上时,点A经过的路径长(即的长)为( )
A、π B、π C、π D、π2. 如图,在Rt△ABC中,∠A=20°,AC=6,将△ABC绕直角顶点C按顺时针方向旋转得到△A′B′C,当点B′第一次落在AB边上时,点A经过的路径长(即的长)为( ) A、 B、 C、2π D、3. 半径为6的圆弧的度数为 , 则它的弧长为( )A、 B、 C、 D、4. 已知扇形的半径为6,圆心角为 , 则此扇形的弧长是( )A、4 B、2 C、 D、5. 勒洛三角形是分别以等边三角形的顶点为圆心,以其边长为半径作圆弧,由三段圆弧组成的曲边三角形.如图,该勒洛三角形绕其中心旋转一定角度后能与自身重合,则该角度可以为( )
A、 B、 C、2π D、3. 半径为6的圆弧的度数为 , 则它的弧长为( )A、 B、 C、 D、4. 已知扇形的半径为6,圆心角为 , 则此扇形的弧长是( )A、4 B、2 C、 D、5. 勒洛三角形是分别以等边三角形的顶点为圆心,以其边长为半径作圆弧,由三段圆弧组成的曲边三角形.如图,该勒洛三角形绕其中心旋转一定角度后能与自身重合,则该角度可以为( ) A、 B、 C、 D、6. 如图,是半圆的直径,、是半圆上两点,且满足 , , 则的长为( )
A、 B、 C、 D、6. 如图,是半圆的直径,、是半圆上两点,且满足 , , 则的长为( )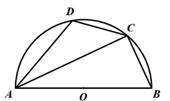 A、 B、 C、 D、7. 如图,已知的半径为6, , 是的弦,若 , 则的长是( )
A、 B、 C、 D、7. 如图,已知的半径为6, , 是的弦,若 , 则的长是( )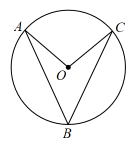 A、 B、10π C、 D、12π8. 如图,为的直径,C是上的一点,若 , , 则的长度为( )
A、 B、10π C、 D、12π8. 如图,为的直径,C是上的一点,若 , , 则的长度为( ) A、 B、 C、 D、9. 如图,正方形的边长为6,将长为的线段的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在上滑动,同时点F在上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段的中点M所经过的路线长为( )
A、 B、 C、 D、9. 如图,正方形的边长为6,将长为的线段的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在上滑动,同时点F在上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段的中点M所经过的路线长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
10. 一个扇形的弧长是 , 半径是 , 则此扇形的圆心角是度.11. 如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么先到达B地
 12. 如图,用一个半径为6cm的定滑轮拉动砝码上升(假设绳索足够长且粗细不计,与滑轮之间无滑动),若滑轮旋转了 , 则砝码上升了cm.(结果保留)
12. 如图,用一个半径为6cm的定滑轮拉动砝码上升(假设绳索足够长且粗细不计,与滑轮之间无滑动),若滑轮旋转了 , 则砝码上升了cm.(结果保留)
三、综合题
-
13. 如图,在中, , , , 以为直径的交于点 , 交于点 , 连接 , 过点作平行于 , 交于点 , 连接、.
 (1)、求证:点为的中点;(2)、求的长度.14. 在平面直角坐标系中,△ABC顶点坐标分别为:A(2,5)、B(-2,3)、C(0,2).线段DE的端点坐标为D(2,-3),E(6,-1).
(1)、求证:点为的中点;(2)、求的长度.14. 在平面直角坐标系中,△ABC顶点坐标分别为:A(2,5)、B(-2,3)、C(0,2).线段DE的端点坐标为D(2,-3),E(6,-1). (1)、线段AB先向平移个单位,再向平移个单位与线段ED重合;(2)、将△ABC绕点P旋转180°后得到的△DEF,使AB的对应边为DE,直接写出点P的坐标,并画出△DEF;(3)、求点C在旋转过程中所经过的路径l的长.15. 如图,△ABC内接于☉O,∠A=60°,BE⊥AC于点E,延长线交☉O于点P。
(1)、线段AB先向平移个单位,再向平移个单位与线段ED重合;(2)、将△ABC绕点P旋转180°后得到的△DEF,使AB的对应边为DE,直接写出点P的坐标,并画出△DEF;(3)、求点C在旋转过程中所经过的路径l的长.15. 如图,△ABC内接于☉O,∠A=60°,BE⊥AC于点E,延长线交☉O于点P。 (1)、如图①,若△ABC是等边三角形,求证:OE=PE;(2)、如图②,当点A在直线BC上方运动时,(包括点B、C)作CQ⊥AB交BE于点H,
(1)、如图①,若△ABC是等边三角形,求证:OE=PE;(2)、如图②,当点A在直线BC上方运动时,(包括点B、C)作CQ⊥AB交BE于点H,①求证:HE=PE
②若BC=3,求点H运动轨迹的长度。