【每日15min】24圆内接正多边形—浙教版数学九（上）微专题精炼

试卷更新日期：2023-10-23 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图，正六边形 $A B C D E F$ 内接于 $⊙ O$ .连接 $B D$ .则 $∠ C D B$ 的度数是（）

A、 $90 °$ B、 $60 °$ C、 $45 °$ D、 $30 °$

查看试题解析
2. 如图是一个半径为6cm的 $⊙ O$ 的纸片， $△ A B C$ 是 $⊙ O$ 的内接三角形，分别以直线 $A B$ 和 $A C$ 折叠 $⊙ O$ 纸片， $\overset{⌢}{A B}$ 和 $\overset{⌢}{A C}$ 都经过圆心O，则图中阴影部分的面积是（　　）

A、 $9 \sqrt{3} c m^{2}$ B、 $8 \sqrt{3} c m^{2}$ C、 $9 \sqrt{6} c m^{2}$ D、 $12 c m^{2}$

查看试题解析
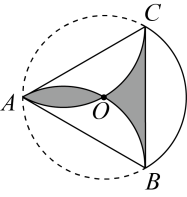3. 如图，正五边形ABCDE内接于⊙O，连接AC，则∠BAC的度数是（）

A、45° B、38° C、36° D、30°

查看试题解析
4. 以半径为4的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是（）．

A、 $\sqrt{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $2 \sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
5. 如图，⊙O是正六边形ABCDEF的外接圆，点P在⊙O上（P不与A，B重合），则∠APB的度数为（）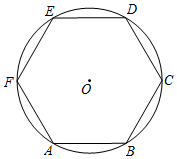

A、60° B、60°或120° C、30° D、30°或150°

查看试题解析
6. 如图，正方形ABCD内接于⊙O，点P在 $\overset{⌢}{A B}$ 上，则下列角中可确定大小的是（　　）

A、∠PCB B、∠PBC C、∠BPC D、∠PBA

查看试题解析
7. 已知下列命题：①抛物线y＝3x²+5x﹣1与两坐标轴交点的个数为2个；②相等的圆心角所对的弦相等；③任何正多边形都有且只有一个外接圆；④三角形的外心到三角形各顶点的距离相等；⑤圆内接四边形对角相等；真命题的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，⊙O是正六边形ABCDEF的外接圆，P是弧AB上一点，则∠CPD的度数是（）

A、30° B、40° C、45° D、60°

查看试题解析

二、填空题

9. 正六边形 $A B C D E F$ 内接于 $⊙ O$ ， $A B = 10 c m$ ，则 $⊙ O$ 的半径是 $c m$ .

查看试题解析
10. 如图，如果AB、AC分别是圆O的内接正三角形和内接正方形的一条边，BC一定是圆O的内接正n边形的一条边，那么n= ．

查看试题解析
11. 若正六边形的外接圆半径长为4，则它的边长等于．

查看试题解析
12. 如图，边长为6的正方形 $A B C D$ 内接于 $⊙ O$ ，点E是 $\overset{⌢}{A B}$ 上的一动点（不与A ， B重合，点F是 $\overset{⌢}{B C}$ 上的一点，连接 $O E ， O F$ ，分别与 $A B ， B C$ 交于点G ， H ，且 $∠ E O F = 90 °$ ，有以下结论：① $O G = O H$ ；② $△ G B H$ 周长的最小值为 $6 + 2 \sqrt{2}$ ；③随着点E位置的变化，四边形 $O G B H$ 的面积始终为9.其中正确的是.（填序号）

查看试题解析

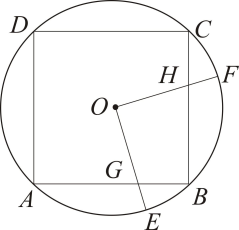
三、解答题

13. 已知圆内接正十二边形的面积为S，求同圆的内接正六边形的面积．

查看试题解析

四、综合题

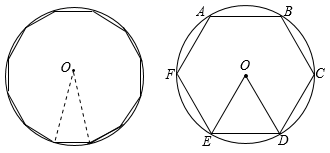
14. 如图，六边形ABCDEF是 $⊙ O$ 的内接正六边形.

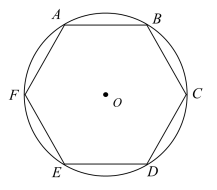(1)、求证：在六边形ABCDEF中，过顶点A的三条对角线四等分 $∠ B A F$ .

(2)、设 $⊙ O$ 的面积为 $S_{1}$ ，六边形ABCDEF的面积为 $S_{2}$ ，求 $\frac{S_{1}}{S_{2}}$ 的值.

查看试题解析
15. 圆周率 $π$ 的故事
我国古代数学家刘徽通过“割圆术”来估计圆周率 $π$ 的值——“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失矣”，可以理解为当正多边形的边数越来越多时，该正多边形与它的外接圆越来越“接近”，这样就可以用正多边形的周长替代它的外接圆的周长，从而估算出圆周率 $π$ 的值.

(1)、对于边长为a的正方形，其外接圆半径为，根据故事中的方法，用该正方形的周长4a替代它的外接圆周长，利用公式 $C = 2 π r$ ，可以估算 $π = \frac{C}{2 r} =$ .

(2)、类比（1），当正多边形为正六边形时，估计 $π$ 的值.

查看试题解析