【每日15min】20垂径定理—浙教版数学九(上)微专题精炼
试卷更新日期:2023-10-23 类型:复习试卷
一、选择题
-
1. 下列语句中不正确的有( )
①长度相等的弧是等弧;②垂直于弦的直径平分弦;③圆是轴对称图形,任何一条直径都是它的对称轴;④平分弦的直线也必平分弦所对的两条弧;⑤半圆是圆中最长的弧;⑥不在同一条直线上的三个点可以确定一个圆.
A、5个 B、4个 C、3个 D、2个2. 已知的半径为 , 若 , 则经过点的弦长可能是( )A、 B、 C、 D、3. 如图,在圆中,弦 , 点在上移动,连接 , 过点做交圆于点 , 则的最大值为( )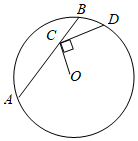 A、 B、2 C、 D、4. 如图,AB为⊙O的弦,OC⊥AB于C,AB=8,OC=3,则⊙O的半径长为( )
A、 B、2 C、 D、4. 如图,AB为⊙O的弦,OC⊥AB于C,AB=8,OC=3,则⊙O的半径长为( ) A、 B、3 C、4 D、55. 如图,在半径为的中,弦 , 是弦上一动点,则的最小值为( )
A、 B、3 C、4 D、55. 如图,在半径为的中,弦 , 是弦上一动点,则的最小值为( ) A、3 B、 C、2 D、16. 如图,点D是直径为10的中一点,若长为3,则过点D的所有弦中,最长弦与最短弦的长度差为( )
A、3 B、 C、2 D、16. 如图,点D是直径为10的中一点,若长为3,则过点D的所有弦中,最长弦与最短弦的长度差为( ) A、2 B、6 C、14 D、187. 一块圆形宣传标志牌如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D.现测得AB=8dm,DC=2dm,则圆形标志牌的半径为( )
A、2 B、6 C、14 D、187. 一块圆形宣传标志牌如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D.现测得AB=8dm,DC=2dm,则圆形标志牌的半径为( ) A、6dm B、5dm C、4dm D、3dm8. 如图,四边形为矩形,AB = 3,BC = 4.点P是线段上一动点,点M为线段AP上一点. , 则的最小值为( )
A、6dm B、5dm C、4dm D、3dm8. 如图,四边形为矩形,AB = 3,BC = 4.点P是线段上一动点,点M为线段AP上一点. , 则的最小值为( )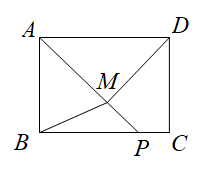 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. ⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB与CD的距离为.10. 如图,已知⊙O的半径为5, , 垂足为 , 且 , 则.
 11. 如图,以原点为圆心的圆过点 , 圆内一个固定点 , 过点作直线,交圆于 , 两点,求的最小值为.
11. 如图,以原点为圆心的圆过点 , 圆内一个固定点 , 过点作直线,交圆于 , 两点,求的最小值为. 12. 五水共治办公室在一次巡查时测量一排水管的排水情况,如图,水平放置的圆柱形排水管的截面为 , 半径是 , 有水部分弓形的高为 , 则.
12. 五水共治办公室在一次巡查时测量一排水管的排水情况,如图,水平放置的圆柱形排水管的截面为 , 半径是 , 有水部分弓形的高为 , 则.
三、作图题
-
13. 如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=8cm,CD=2cm.
 (1)、尺规作图作出此残片所在的圆;(不写作法,保留作图痕迹)(2)、求(1)中所作圆的半径.
(1)、尺规作图作出此残片所在的圆;(不写作法,保留作图痕迹)(2)、求(1)中所作圆的半径.四、解答题
-
14. “筒车”是一种以水流作动力,取水灌田的工具.明朝科学家徐光启在农政全书中用图画描绘了“筒车”的工作原理.如图,“筒车”盛水筒的运行轨迹是以轴心为圆心的圆,已知圆心始终在水面上方,且当圆被水面截得的弦为6米时,水面下盛水筒的最大深度为1米即水面下方部分圆上一点距离水面的最大距离.
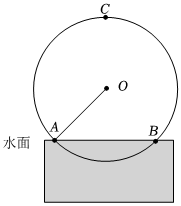 (1)、求该圆的半径;(2)、若水面上涨导致圆被水面截得的弦从原来的6米变为8米时,则水面下盛水筒的最大深度为多少米?15. 根据以下素材,探索完成任务.
(1)、求该圆的半径;(2)、若水面上涨导致圆被水面截得的弦从原来的6米变为8米时,则水面下盛水筒的最大深度为多少米?15. 根据以下素材,探索完成任务.如何设计高架桥的限高及车道宽方案?
素材1
图1高架桥是一段圆弧拱形结构,图2是它的示意图.经测量,拱形跨度24m,拱顶离地面6m.

素材2
如图3,某道路规划部门计划将左侧公路分为非机动车道、机动车道一、机动车道二及绿化带四部分,原计划设计非机动车道宽3m,每条机动车道宽均3.5m.为了保证车辆的行驶安全,高架下方需要设置限高标志以警示车辆驾驶员.(限高即图中FC的高度)

素材3
如图4,由于城市道路绿化需求,道路规划部门确定新方案为在非机动车道和机动车道一之间增加一条宽为1m的绿化带,中间绿化带宽度不变,每条机动车道道宽均不小于3.25m且相等,非机动车道最高高度不小于2.5m.

问题解决
任务1
确定桥拱所在圆弧的半径.
在图2中补好图形,标注字母、数据等信息,求出桥拱所在圆弧的半径长.
任务2
探究原计划该高架桥下方机动车道一的限高要求.
在图3中画出图形,标注字母、数据等信息,计算确定机动车道一的限高高度.
任务3
拟定新方案下非机动车道和机动车车道宽度.
给出一对符合新方案要求的非机动车道和机动车道的道宽值.
(参考数值:=9.63,=11.61)
-