2023-2024学年北师大版数学七年级上学期期中仿真模拟试卷(三)
试卷更新日期:2023-10-23 类型:期中考试
一、单选题(每题3分,共30分)
-
1. ﹣ 的相反数是( )A、 B、﹣6 C、6 D、﹣2. 小云同学在“百度”搜索引擎中输入“北京2022冬奥会”,能找到相关结果约为42500000个,将42500000用科学记数法表示应为()A、 B、 C、 D、3. 冰箱冷藏室的温度零上3℃,记作+3℃,则冷冻室的温度零下17℃,记作( )A、20℃ B、-20℃ C、17℃ D、-17℃4. 圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列如图是以下四个图中的哪一个绕着直线旋转一周得到的( )
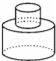 A、
A、 B、
B、 C、
C、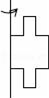 D、
D、 5. 如图,直角三角尺中阴影部分的面积可以表示为( )
5. 如图,直角三角尺中阴影部分的面积可以表示为( ) A、ab-πr2 B、-πr2 C、ab-2πr D、-2πr26. 有理数a,b在数轴上的位置如图所示,则下列各式:
A、ab-πr2 B、-πr2 C、ab-2πr D、-2πr26. 有理数a,b在数轴上的位置如图所示,则下列各式:①a+b>0;②a﹣b>0;③|b|>a;④ab<0.一定成立的是( )
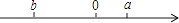 A、①②③ B、③④ C、②③④ D、①③④7. 如果和互为相反数,那么的值是( )A、-2017 B、2017 C、-1 D、18.
A、①②③ B、③④ C、②③④ D、①③④7. 如果和互为相反数,那么的值是( )A、-2017 B、2017 C、-1 D、18.如图,将正方体相邻的两个面上分别画出3×3的正方形网格,并分别用图形“
 ”和“○”在网格内的交点处做上标记,则该正方体的表面展开图是( )
”和“○”在网格内的交点处做上标记,则该正方体的表面展开图是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 下列计算中错误的是( )A、 B、 C、 D、10. 按如图所示的运算程序,若输入x=2,y=1,则输出结果为( )
9. 下列计算中错误的是( )A、 B、 C、 D、10. 按如图所示的运算程序,若输入x=2,y=1,则输出结果为( ) A、1 B、4 C、5 D、9
A、1 B、4 C、5 D、9二、填空题(每题3分,共15分)
-
11. 比较大小;-|-0.4|-(-0.4).(填“<”、“=”、“>”)12. 某种水果的售价为每千克a元,用面值为50元的人民币购买了3千克这种水果,应找回 元(用含a的代数式表示).13. 若a,b互为相反数, 互为倒数,则 的值是 .14. 定义 ,若 ,则 x 的值为.15. 下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,……,则第⑩个图形中棋子的颗数为.



三、解答题(共7题,共55分)
-
16. 在数轴上表示下列各数: ,并用“<”号把这些数连接起来.17. 计算:(1)、23-17-(-7)+(-13)(2)、(3)、(4)、18. 定义一种新运算“ ”,规则为: ,例如: ,解答下列问题:(1)、 ;(2)、 .19. 如图是由7个同样大小的小正方体搭成的几何体,请在下面方格纸中分别画出这个几何体从正面看、从左面看、从上面看的形状图(提示:在答题卡上先用铅笔和直尺作图,检查正确后再用黑色中性签字笔描图)
 20. 如图,A和B是高度同为h的圆柱形容器,底面半径分别为r和R,且r<R.一龙头单独向A注水,用T分钟可以注满容器A.现将两容器在他们高度的一半处用一个细管连通(连通细管的容积忽略不计),仍用该水龙头向注水A,问2T分钟时,容器A中水的高度是多少?(注:若圆柱体底面积半径为R,高为h,体积为V,则V=πR2h.)
20. 如图,A和B是高度同为h的圆柱形容器,底面半径分别为r和R,且r<R.一龙头单独向A注水,用T分钟可以注满容器A.现将两容器在他们高度的一半处用一个细管连通(连通细管的容积忽略不计),仍用该水龙头向注水A,问2T分钟时,容器A中水的高度是多少?(注:若圆柱体底面积半径为R,高为h,体积为V,则V=πR2h.) 21. 某出租汽车从停车场出发沿着东西向的大街进行汽车出租,到晚上6时,一天行驶记录如下:(向东记为正,向西记为负,单位:千米)
21. 某出租汽车从停车场出发沿着东西向的大街进行汽车出租,到晚上6时,一天行驶记录如下:(向东记为正,向西记为负,单位:千米)+10,﹣3,+4,+2,+8,+5,﹣2,﹣8,+12,﹣5,﹣7.
(1)、到晚上6时,出租车在停车场的什么方向?相距多远?(2)、若汽车每千米耗油0.2升,则从停车场出发到晚上6时,出租车共耗油多少升?22. 综合应用题:的几何意义是数轴上表示m的点与表示n的点之间的距离.
(1)、的几何意义是数轴上表示的点与之间的距离,;(选填“>”“<”或“=”)(2)、几何意义是数轴上表示2的点与表示1的点之间的距离,则;(3)、的几何意义是数轴上表示的点与表示的点之间的距离,若 , 则;(4)、的几何意义是数轴上表示的点与表示的点之间的距离,若 , 则;(5)、找出所有符合条件的整数x , 使得这样的整数是 .