2023-2024学年北师大版数学七年级上学期期中仿真模拟试卷(二)
试卷更新日期:2023-10-23 类型:期中考试
一、单选题(每题3分,共30分)
-
1. 下列四个数中,最小的是( )A、|﹣1.5| B、0 C、﹣(﹣3) D、﹣32. 据旅游研究院最新数据显示,今年中秋节国庆节假期,全国实现旅游收入210500000000元,将旅游收入210500000000元用科学记数法表示为( ).A、 元 B、 元 C、 元 D、 元3. 用一个平面去截一个几何体,如果截面是三角形,那么这个几何体不可能是( )A、圆柱 B、长方体 C、圆锥 D、三棱柱4. 下列结论中,正确的是( )A、单项式的系数是3 B、单项式的系数是 , 次数是4 C、与是同类项 D、多项式是三次三项式5. 有理数a、b在数轴上的位置如图所示,那么下列式子中成立的是( )
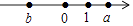 A、1﹣b>a B、a<b C、ab>0 D、 >06. 如图,将小正方体切去一个角后再展开,其平面展开图正确的是( )
A、1﹣b>a B、a<b C、ab>0 D、 >06. 如图,将小正方体切去一个角后再展开,其平面展开图正确的是( )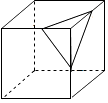 A、
A、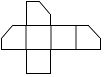 B、
B、 C、
C、 D、
D、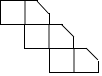 7. 某服装2014年10月底的价格是每件a元,受市场影响,2014年元旦前价格平均下降了10%,到了春节前平均又上升了15%,则春节前的售价是每件( )A、(1﹣10%)(1+15%)a元 B、(1﹣10%)15%a元 C、(1+10%)(1﹣15%)a元 D、(1+10%)15%a元8. 多项式-x3﹣4x2+x+1与多项式3x3+2mx2﹣5x+3相加后不含二次项,则m的值为( )A、2 B、﹣2 C、4 D、﹣49. 下列说法正确的个数有( )(1)、若 , 则;(2)若a,b互为相反数,则;(3)绝对值相等的两数相等;(4)单项式的次数是6;(5)一定是一个负数.A、4 B、3 C、2 D、110. 任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和,如: , , , …按此规律,若分裂后,其中有一个奇数是2023,则m的值是( )A、46 B、45 C、44 D、43
7. 某服装2014年10月底的价格是每件a元,受市场影响,2014年元旦前价格平均下降了10%,到了春节前平均又上升了15%,则春节前的售价是每件( )A、(1﹣10%)(1+15%)a元 B、(1﹣10%)15%a元 C、(1+10%)(1﹣15%)a元 D、(1+10%)15%a元8. 多项式-x3﹣4x2+x+1与多项式3x3+2mx2﹣5x+3相加后不含二次项,则m的值为( )A、2 B、﹣2 C、4 D、﹣49. 下列说法正确的个数有( )(1)、若 , 则;(2)若a,b互为相反数,则;(3)绝对值相等的两数相等;(4)单项式的次数是6;(5)一定是一个负数.A、4 B、3 C、2 D、110. 任意大于1的正整数m的三次幂均可“分裂”成m个连续奇数的和,如: , , , …按此规律,若分裂后,其中有一个奇数是2023,则m的值是( )A、46 B、45 C、44 D、43二、填空题(每空3分,共15分)
-
11. 子弹从枪膛中射出去的轨迹可看成一条线,这说明 的数学道理.12. ,则 的值为.13. 若 与 是同类项,则 .14. 当时,代数式的值为15. 用(x,y)表示x,y两数中较大的一个数,用[x,y]表示x,y两数中较小的一个数,则(﹣5,﹣0.5)﹣[﹣3,2]的值为 .
三、解答题(共7题,共55分)
-
16. 计算:(1)、6+(﹣8)﹣3+(﹣5);(2)、(﹣3)﹣(﹣5)+(﹣4)﹣4;(3)、()×(﹣36);(4)、3+50÷22×()﹣1.17. 化简求值: , 其中 , .18. 从正面、左面、上面观察如图所示的几何体,分别画出你所看到的几何体的形状图.
 19. 国庆黄金周电影《长津湖》成为了浙江人民观影的首选,宁波某区9月30日该电影票的售票量为 万张,该区10月1日到10月7日售票量的变化如下表(正号表示售票量比前一天多,负号表示售票量比前一天少):
19. 国庆黄金周电影《长津湖》成为了浙江人民观影的首选,宁波某区9月30日该电影票的售票量为 万张,该区10月1日到10月7日售票量的变化如下表(正号表示售票量比前一天多,负号表示售票量比前一天少):日期
1 日
2 日
3 日
4 日
5 日
6 日
7 日
售票量的变化(单位:万张)
+0.5
+0.1
-0.3
-0.2
+0.4
-0.2
+0.1
请根据以上信息, 回答下列问题:
(1)、10月2日的售票量为多少万张?(2)、10月7日与9月30日相比较, 哪一天的售票量多? 多多少万张?(3)、若平均每张票价为50元,则10月1日到10月7日该区销售 长津湖》电影票共收入多少万元?20. 阅读理解,a、b、c、d是实数,我们把符号 称为2×2行列式,并且规定 =a×d-b×c,例如, =3×(-2)-2×1=-6-2=-8,问题:
(1)、计算 = .(2)、若x2+4x=4,计算 的值.21. 相传大禹治水时,“洛水”中出现了一个神龟,其背上有美妙的图案,史称“洛书”.用现在的数字翻译出来,就是三阶幻方.三阶幻方是最简单的幻方,又叫九宫格,其对角线、横行、纵向的数字之和均相等,这个和叫做幻和,正中间那个数叫中心数,且幻和恰好等于中心数的3倍.如图1,是由1、2、3、4、5、6、7、8、9所组成的一个三阶幻方,其幻和为15,中心数为5. (1)、如图2所示,则幻和=;(2)、若 , , 求a的值;(3)、由三阶幻方可以衍生出许多有特定规律的新幻方.在如图3所示的“幻方”中,每个小三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等,当 , 时,则的值为多少?22. 在数轴上有A、B两点,点B表示的数为b.对点A给出如下定义:当时,将点A向右移动2个单位长度,得到点P;当时,将点A向左移动个单位长度,得到点P.称点P为点A关于点B的“伴侣点”.如图,点A表示的数为.
(1)、如图2所示,则幻和=;(2)、若 , , 求a的值;(3)、由三阶幻方可以衍生出许多有特定规律的新幻方.在如图3所示的“幻方”中,每个小三角形的三个顶点上的数字之和都与中间正方形四个顶点上的数字之和相等,当 , 时,则的值为多少?22. 在数轴上有A、B两点,点B表示的数为b.对点A给出如下定义:当时,将点A向右移动2个单位长度,得到点P;当时,将点A向左移动个单位长度,得到点P.称点P为点A关于点B的“伴侣点”.如图,点A表示的数为.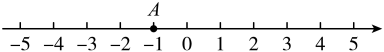 (1)、在图中画出当时,点A关于点B的“伴侣点”P;(2)、当点P表示的数为-6,若点P为点A关于点B的“伴侣点”,则点B表示的数;(3)、点A从数轴上表示-1的位置出发,以每秒1个单位的速度向右运动,点B从数轴上表示8的位置同时出发,以每秒2个单位的速度向左运动,两个点运动的时间为t秒.
(1)、在图中画出当时,点A关于点B的“伴侣点”P;(2)、当点P表示的数为-6,若点P为点A关于点B的“伴侣点”,则点B表示的数;(3)、点A从数轴上表示-1的位置出发,以每秒1个单位的速度向右运动,点B从数轴上表示8的位置同时出发,以每秒2个单位的速度向左运动,两个点运动的时间为t秒.①点B表示的数为 (用含t的式子表示);
②是否存在t,使得此时点A关于点B的“伴侣点”P恰好与原点重合?若存在,请求出t的值;若不存在,请说明理由.