2023-2024学年北师大版数学八年级上学期期中仿真模拟试卷(三)
试卷更新日期:2023-10-23 类型:期中考试
一、选择题(每题3分,共10小题,共30分每题只有一个正确选项)
-
1. 下列各数是无理数的是( )A、0.3333 B、-2 C、 D、2. 下列说法错误的是( )A、1的平方根是±1 B、-1的立方根是-1 C、是2的平方根 D、-3是的平方根3. 下列各组三条线段组成的三角形不是直角三角形的是( )A、2,3,4 B、5,12,13 C、6,8,10 D、3,4,54. 在平面直角坐标系中,将点A(-1,-4)向右平移3个单位长度后得到的点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是( )A、(66,34) B、(67,34) C、(100,33) D、(99,34)6. 估计的运算结果应在( )A、5到6之间 B、6到7之间 C、7到8之间 D、8到9之间7. 在国内投寄平信应付邮资如下表:
信件质量 克
邮资 元 封
则y关于x的函数图象正确的是( )
A、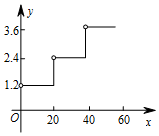 B、
B、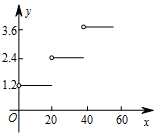 C、
C、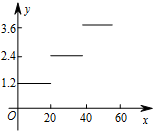 D、
D、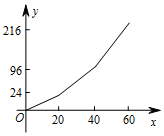 8.
8.如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是( )
 A、CD、EF、GH B、AB、EF、GH C、AB、CD、GH D、AB、CD、EF9. 如图,在Rt△ABC中,∠ACB=90°,AB=4.分别以AC,BC为直径作半圆,面积分别记为S1 , S2 , 则S1+S2的值等于( )
A、CD、EF、GH B、AB、EF、GH C、AB、CD、GH D、AB、CD、EF9. 如图,在Rt△ABC中,∠ACB=90°,AB=4.分别以AC,BC为直径作半圆,面积分别记为S1 , S2 , 则S1+S2的值等于( )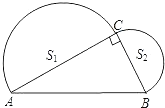 A、2π B、3π C、4π D、8π10. 如图,在△ABC中,∠BAC=90°,AB=AC=4,若点D为BC的中点,过点D作∠MDN=90°,分别交AB,AC于点M,N,连接AD,则下的出论中:①△DMN是等腰直角三角形;②△DMN的周长有最小值;③四边形AMDN的面积为定值8;④△DMN的面积有最小值。正确的有( )
A、2π B、3π C、4π D、8π10. 如图,在△ABC中,∠BAC=90°,AB=AC=4,若点D为BC的中点,过点D作∠MDN=90°,分别交AB,AC于点M,N,连接AD,则下的出论中:①△DMN是等腰直角三角形;②△DMN的周长有最小值;③四边形AMDN的面积为定值8;④△DMN的面积有最小值。正确的有( )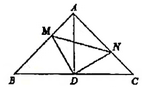 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题(本大题共5小題,每小题3分,共15分)
-
11. 若8的平方根和立方根分别是 和 ,则 .12. 点 关于 轴的对称点的坐标是.13. 已知 的周长是4+4 ,斜边上的中线长是2,则 .14. 某市出租车的收费起步价为14元,即路程不超过3公里时收费14元,超过部分每公里收费2.4元.如果乘客乘坐出租车行驶的路程为x(x>3)公里,乘车费为y元,那么y与x之间的关系式为 .15. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若ab=8,大正方形的面积为25,则小正方形的边长为.

三、解答题(本大题共7小题,其中第16题12分,第17题5分,第18题6分,第19题6分,第20题7分,第21题9分,第22题10分,共55分)
-
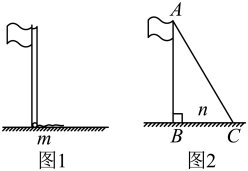
16. 计算下列各题(1)、(2)、(3)、(4)、17. 如图,数学兴趣小组要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面并多出一段(如图1),聪明的小红发现:先测出垂到地面的绳子长,再将绳子拉直(如图2),测出绳子末端C到旗杆底部B的距离n , 利用所学知识就能求出旗杆的长,若米,米,求旗杆的长.
 18. 如图,平面直角坐标系中,的顶点都在网格点上,其中 , , .
18. 如图,平面直角坐标系中,的顶点都在网格点上,其中 , , . (1)、作出关于y轴对称的;(2)、求的面积;(3)、在x轴上是否存在一点P,使的和最短?如果存在,请求出此时的值;如果不存在,请说明理由.19. 如图:在中, , 高 , 动点P由点C沿向点B运动(不与点B重合),设的长为x , 的面积为S .
(1)、作出关于y轴对称的;(2)、求的面积;(3)、在x轴上是否存在一点P,使的和最短?如果存在,请求出此时的值;如果不存在,请说明理由.19. 如图:在中, , 高 , 动点P由点C沿向点B运动(不与点B重合),设的长为x , 的面积为S . (1)、在这个过程中,常量有变量有(2)、请写出S与x之间的函数关系式,并指出自变量x的取值范围(3)、当x取时计算此时的S值(4)、S为时,求出对应x的值20. 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点。
(1)、在这个过程中,常量有变量有(2)、请写出S与x之间的函数关系式,并指出自变量x的取值范围(3)、当x取时计算此时的S值(4)、S为时,求出对应x的值20. 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点。 (1)、求证:△ACE≌△BCD:(2)、若CB= , AD=2,求DE的长.21. 如图,在平面直角坐标系中,一次函数的图象经过点 , 与轴和轴分别相交于点和点 , 与正比例函数的图象相交于点 , 点的纵坐标为3.
(1)、求证:△ACE≌△BCD:(2)、若CB= , AD=2,求DE的长.21. 如图,在平面直角坐标系中,一次函数的图象经过点 , 与轴和轴分别相交于点和点 , 与正比例函数的图象相交于点 , 点的纵坐标为3.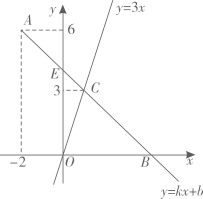 (1)、求一次函数的解析式;(2)、若点在轴上,满足 , 求点的坐标.(3)、若直线与的三边有两个公共点,则的取值范围是 .22. 如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为1秒.
(1)、求一次函数的解析式;(2)、若点在轴上,满足 , 求点的坐标.(3)、若直线与的三边有两个公共点,则的取值范围是 .22. 如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为1秒. (1)、出发2秒后,求PQ的长;(2)、当点Q在边BC上运动时,出发几秒钟,APQB能形成等腰三角形?(3)、当点Q在边CA上运动时,求能使ABCQ成为等腰三角形的运动时间(直接写出答案).
(1)、出发2秒后,求PQ的长;(2)、当点Q在边BC上运动时,出发几秒钟,APQB能形成等腰三角形?(3)、当点Q在边CA上运动时,求能使ABCQ成为等腰三角形的运动时间(直接写出答案).