2023-2024学年北师大版数学八年级上学期期中仿真模拟试卷(一)
试卷更新日期:2023-10-23 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 下列各数中,是无理数的是( )A、 B、3.14 C、 D、02. 以下能够准确表示我校地理位置的是( )A、离宁波市主城区10千米 B、在江北区西北角 C、在海曙以北 D、东经 , 北纬3. 如图,数轴上的点P表示下列四个无理数中的一个,这个无理数是( )
 A、 B、 C、 D、4. 已知△ABC的三边分别是a、b、c,下列条件中不能判断△ABC为直角三角形的是( )A、a2+b2=c2 B、∠A:∠B:∠C=3:4:5 C、∠A=∠C-∠B D、a=1,b=2,c=5. 下列说法错误的是( )A、的算术平方根是 B、是的平方根 C、的立方根是 D、是的平方根6. 下列图象中,表示y是x的函数的是( )A、
A、 B、 C、 D、4. 已知△ABC的三边分别是a、b、c,下列条件中不能判断△ABC为直角三角形的是( )A、a2+b2=c2 B、∠A:∠B:∠C=3:4:5 C、∠A=∠C-∠B D、a=1,b=2,c=5. 下列说法错误的是( )A、的算术平方根是 B、是的平方根 C、的立方根是 D、是的平方根6. 下列图象中,表示y是x的函数的是( )A、 B、
B、 C、
C、 D、
D、 7. 函数的图象向左平移2个单位,相应的函数表达式为( )A、 B、 C、 D、8. 如图,所有阴影部分的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C的面积依次为6、10、7,则正方形D的面积为( )
7. 函数的图象向左平移2个单位,相应的函数表达式为( )A、 B、 C、 D、8. 如图,所有阴影部分的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C的面积依次为6、10、7,则正方形D的面积为( ) A、11 B、16 C、17 D、239. 直线与在同一平面直角坐标系内,其位置可能是( )A、
A、11 B、16 C、17 D、239. 直线与在同一平面直角坐标系内,其位置可能是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,已知 中, , ,在BC边上取一点P(点P不与点B、C重合),使得 成为等腰三角形,则这样的点P共有( ).
10. 如图,已知 中, , ,在BC边上取一点P(点P不与点B、C重合),使得 成为等腰三角形,则这样的点P共有( ). A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题3分,共15分)
-
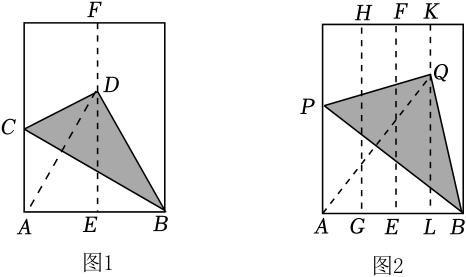
11. 现定义一个新运算“※”,规定对于任意实数x,y,都有 , 则的值为 .12. 如图1,小明将一张长方形纸片对折,使长方形两边重合,折痕为EF,铺开后沿BC折叠,使点A与EF上的点D重合.如图2,再将该长方形纸片进行折叠,折痕分别为HG,KL,使长方形的两边均与EF重合;铺开后沿BP折叠,使点A与KL上的点Q重合;分别连结图1中的AD与图2中的AQ,则的值为.
 13. 如图,已知直线l经过点(0,-1)并且垂直于y轴,若点P(-3,2)与点Q(a,b)关于直线l对称,则a+b= .
13. 如图,已知直线l经过点(0,-1)并且垂直于y轴,若点P(-3,2)与点Q(a,b)关于直线l对称,则a+b= .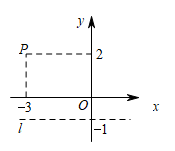 14. 如图,直线()过点 , 则关于的方程的解为;
14. 如图,直线()过点 , 则关于的方程的解为; 15. 如图是某路口处草坪的一角,当行走路线是时,有人为了抄近道而避开路的拐角 , 于是在草坪内走出了一条不该有的捷径路.某学习实践小组通过测量可知,的长约为6米,的长约为8米,为了提醒居民爱护草坪,他们想在A,处设立“踏破青白可惜,多行数步无妨”的提示牌.则提示牌上的“多行数步”是指多行米.
15. 如图是某路口处草坪的一角,当行走路线是时,有人为了抄近道而避开路的拐角 , 于是在草坪内走出了一条不该有的捷径路.某学习实践小组通过测量可知,的长约为6米,的长约为8米,为了提醒居民爱护草坪,他们想在A,处设立“踏破青白可惜,多行数步无妨”的提示牌.则提示牌上的“多行数步”是指多行米.
三、解答题(共7题,共55分)
-
16. 计算:(1)、(2)、(3)、17. 如图,有一架秋千,当它静止时,踏板离地的垂直高度 , 将它往前推送水平距离时,秋千的踏板离地的垂直高度 , 若秋干的绳索始终拉得很直,求绳索的长度.
 18. 阅读下面的文字,解答问题:是一个无理数,而无理数是无限不循环小数,因此的小数部分无法全部写出来,但是我们可以想办法把它表示出来因为 , 所以的整数部分为1,将减去其整数部分后,得到的差就是小数部分,于是的小数部分为 . 请解答下列问题:(1)、的整数部分是 , 小数部分是;(2)、如果的小数部分为a,的小数部分为b,若 , 求x的值.19. 定义:如图,点M,N把线段AB分割成AM,MN,NB,若以AM,MN,NB为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
18. 阅读下面的文字,解答问题:是一个无理数,而无理数是无限不循环小数,因此的小数部分无法全部写出来,但是我们可以想办法把它表示出来因为 , 所以的整数部分为1,将减去其整数部分后,得到的差就是小数部分,于是的小数部分为 . 请解答下列问题:(1)、的整数部分是 , 小数部分是;(2)、如果的小数部分为a,的小数部分为b,若 , 求x的值.19. 定义:如图,点M,N把线段AB分割成AM,MN,NB,若以AM,MN,NB为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点. (1)、已知M,N把线段AB分割成AM,MN,NB,若AM= 1,MN=2,BN= , 则点M,N是线段AB的勾股分割点吗?请说明理由.(2)、已知点M,N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.20. 如图1,在同一平面直角坐标系中,直线:与直线:相交于点 , 与x轴交于点 , 直线与轴交于点.
(1)、已知M,N把线段AB分割成AM,MN,NB,若AM= 1,MN=2,BN= , 则点M,N是线段AB的勾股分割点吗?请说明理由.(2)、已知点M,N是线段AB的勾股分割点,且AM为直角边,若AB=12,AM=5,求BN的长.20. 如图1,在同一平面直角坐标系中,直线:与直线:相交于点 , 与x轴交于点 , 直线与轴交于点. (1)、填空: = , = , = ;(2)、如图2,点为线段上一动点,将△沿直线翻折得到△ , 线段交轴于点.
(1)、填空: = , = , = ;(2)、如图2,点为线段上一动点,将△沿直线翻折得到△ , 线段交轴于点.① 当点落在轴上时,求点的坐标;
② 若△为直角三角形,求点的坐标.
21. 勾股定理是初等几何中最重要的定理之一,它的证明方法很多,如图1是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,通过对图形的切割、拼接,巧妙的利用面积关系证明了勾股定理. (1)、定理证明:
(1)、定理证明:图1是由四个全等的直角三角形围成的一个大正方形,中间的部分是一个小正方形(阴影).如果直角三角形较小的直角边长为a,较大的直角边长为b,斜边长为c,请你根据图1证明勾股定理;
(2)、问题解决:如图2,圆柱的底面半径为 , 高为 , 蚂蚁在圆柱表面爬行,从点A爬到点B的最短路程是多少厘米?(结果保留π)
22. 如图,已知直线与x轴、y轴分别交于两点,直线与y轴交于点C,与直线交于点D. (1)、求直线的表达式;(2)、点P是线段上一点,连接 , 当的面积为9,求P点坐标;(3)、若正比例函数的图象与直线交于点P,且点O、点P到直线的距离相等,请直接写出符合条件的m的值.
(1)、求直线的表达式;(2)、点P是线段上一点,连接 , 当的面积为9,求P点坐标;(3)、若正比例函数的图象与直线交于点P,且点O、点P到直线的距离相等,请直接写出符合条件的m的值.