2023-2024学年北师大版数学九年级上学期期中仿真模拟试卷(二)
试卷更新日期:2023-10-23 类型:期中考试
一、选择题(共10小题,每小题3分)
-
1. 下列方程中,是一元二次方程的是( )A、 B、 C、 D、2. 如图中几何体的左视图是( )
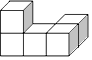 A、
A、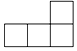 B、
B、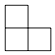 C、
C、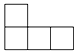 D、
D、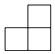 3. 已知:关于x的方程有实根,则m的取值范围为( )A、且 B、且 C、 D、4. 已知反比例函数 , 下列各点中,在此函数图象上的点的是( )A、( , 1) B、(2,2) C、(1,2) D、(2,)5. 连续抛掷两枚质地均匀的硬币,“两枚正面朝上”的概率是( )A、 B、 C、 D、16. 如图,点 , 在线段 上, 与 全等,点 和点 ,点 和点 是对应点, 和 交于点 ,则与 相等的线段是( )
3. 已知:关于x的方程有实根,则m的取值范围为( )A、且 B、且 C、 D、4. 已知反比例函数 , 下列各点中,在此函数图象上的点的是( )A、( , 1) B、(2,2) C、(1,2) D、(2,)5. 连续抛掷两枚质地均匀的硬币,“两枚正面朝上”的概率是( )A、 B、 C、 D、16. 如图,点 , 在线段 上, 与 全等,点 和点 ,点 和点 是对应点, 和 交于点 ,则与 相等的线段是( )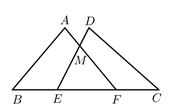 A、 B、 C、 D、7. 为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为289元的药品进行连续两次降价后为256元,设平均每次降价的百分率为x , 则下面所列方程正确的是( )A、 B、 C、 D、8. 若一元二次方程的一个根是x=1,则的值是( )A、-1 B、0 C、1 D、不能确定9. 若点A(1, ),B(2, )在反比例函数 的图象上.则 , 的大小关系是( ).A、 B、 C、 D、10. 边长为4的正方形ABCD中,对角线AC,BD交于点O,E在
A、 B、 C、 D、7. 为解决群众看病贵的问题,有关部门决定降低药价,对某种原价为289元的药品进行连续两次降价后为256元,设平均每次降价的百分率为x , 则下面所列方程正确的是( )A、 B、 C、 D、8. 若一元二次方程的一个根是x=1,则的值是( )A、-1 B、0 C、1 D、不能确定9. 若点A(1, ),B(2, )在反比例函数 的图象上.则 , 的大小关系是( ).A、 B、 C、 D、10. 边长为4的正方形ABCD中,对角线AC,BD交于点O,E在BD上,作EF⊥CE交AB于点F,连接CF交BD于H,则下列结论:①EF=EC;②;③;④若BF=1,则 , 正确的是( )
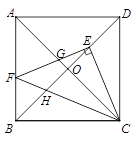 A、①②④ B、②③④ C、①②③ D、①②③④
A、①②④ B、②③④ C、①②③ D、①②③④二、填空题(共5小题,每小题3分)
-
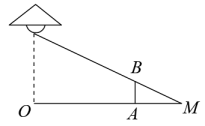
11. 一元二次方程 的解是 .12. 如果 , 那么 .13. 在一个不透明的布袋中装有红球、白球共20个,它们除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红球的频率稳定在0.6,则随机从布袋中摸出一个球是红球的概率是.14. 如图,路灯距离地面6米,身高1.2米的小明站在距离路灯的底部(点O)10米的A处,则小明的影长为米.
 15. 如图,点A(m,6),B(n,1)在反比例函数 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是 .
15. 如图,点A(m,6),B(n,1)在反比例函数 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是 .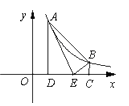
三、解答题(共7小题,共55分,其中16题12分,17题6分,18题8分,19题6分,20题7分,21题9分,22题7分)
-
16. 解下列一元二次方程:(1)、-x2+4x-3=0(配方法)(2)、 ;(3)、 ;(4)、3x(x-1)=2-2x.17. 某校八年级计划在开学第二周的星期二至星期五开展社会实践活动,要求每位学生选择两天参加活动.(1)、乙同学随机选择连续的两天,其中有一天是星期三的概率是 ;(2)、甲同学随机选择两天,请用列表或画树状图的方法求其中有一天是星期三的概率.18. 如图,在平面直角坐标系中,ABC 的三个顶点坐标分别为A(-2,1)、B(-1,4)、C(-3,3)
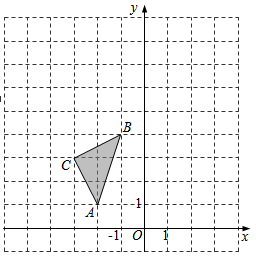
(1)画出ABC关于y轴对称的A1B1C1;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出将ABC放大后的A2B2C2;直接写出点C2的坐标.
19. 雨后的一天晚上,小明和小彬想利用自己所学的测量物体的高度的相关知识,测量路灯的高度AB,如图所示,当小明直立在点C处时,小彬测得小明的影子CE的长为4米;此时小明恰好在他前方2米的点F处的小水源中看到路灯点A的影子已知小明的身高为1.7米,请你利用以上数据求出路灯的高度AB.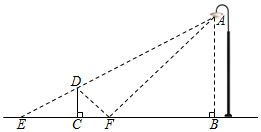 20. 如图,在△ABC中,∠ACB = 90°,D是BC的中点,过点C作CE⊥AD,交AD于点E,交AB于点F,作点E关于直线AC的对称点G,连接AG和GC,过点B作BM⊥GC交GC的延长线于点M .
20. 如图,在△ABC中,∠ACB = 90°,D是BC的中点,过点C作CE⊥AD,交AD于点E,交AB于点F,作点E关于直线AC的对称点G,连接AG和GC,过点B作BM⊥GC交GC的延长线于点M .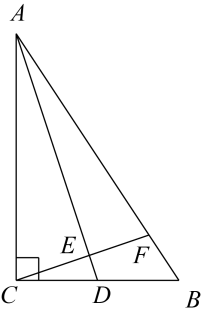 (1)、① 根据题意,补全图形;
(1)、① 根据题意,补全图形;② 比较∠BCF与∠BCM的大小,并证明.
(2)、过点B作BN⊥CF交CF的延长线于点N,用等式表示线段AG,EN与BM的数量关系,并证明.21. 如图1所示,在四边形ABCD中,点O,E,F,G分别是AB,BC,CD,AD的中点,连接OE,EF,FG,GO,GE.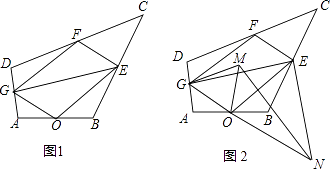 (1)、证明:四边形OEFG是平行四边形;
(1)、证明:四边形OEFG是平行四边形;
(2)、将△OGE绕点O顺时针旋转得到△OMN,如图2所示,连接GM,EN.①若OE= ,OG=1,求 的值;
②试在四边形ABCD中添加一个条件,使GM,EN的长在旋转过程中始终相等.(不要求证明)
22. 如图,在矩形中, , 分别以所在直线为轴、轴,建立平面直角坐标系,是边上的一个动点(不与重合),反比例函数 的图象经过点且与边交于点 , 作直线 .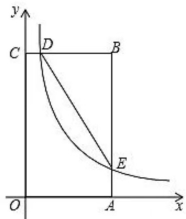
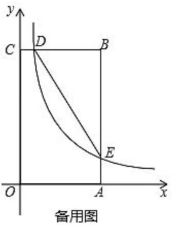 (1)、当点运动到中点时,求的值;(2)、求的值;(3)、连接 , 当的面积为时,求值.
(1)、当点运动到中点时,求的值;(2)、求的值;(3)、连接 , 当的面积为时,求值.