2023-2024学年北师大版数学九年级上学期期中仿真模拟试卷（一）

试卷更新日期：2023-10-23 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图，已知菱形 $A B C D$ 的边长为2， $∠ D A B = 60 °$ ，则对角线 $B D$ 的长是（）

A、1 B、4 C、2 D、6

查看试题解析
2. 如图，平行四边形 $A B C D$ 中，对角线AC ， BD相交于点O ， $O A = 2$ ，若要使平行四边形 $A B C D$ 为矩形，则BD的长应该为（）

A、4 B、3 C、2 D、1

查看试题解析
3. 关于x的方程 $(2 - m) x^{m^{2} - 2} + 5 x - 3 = 0$ 是一元二次方程，则m等于（）

A、0 B、－2 C、2 D、±2

查看试题解析
4. 某种植基地 $2016$ 年蔬菜产量为 $80$ 吨，预计 $2018$ 年蔬菜产量达到 $100$ 吨，求蔬菜产量的年平均增长率，设蔬菜产量的年平均增长率为 $x$ ，则可列方程为（）

A、 $80 (1 + x)^{2} = 100$ B、 $100 (1 - x)^{2} = 80$ C、 $80 (1 + 2 x) = 100$ D、 $80 (1 + x^{2}) = 100$

查看试题解析
5. 一个袋子中装有12个球（袋中每个球除颜色外其余都相同）．其活动小组想估计袋子中红球的个数，分10个组进行摸球试验，每一组做400次试验，汇总后，摸到红球的次数为3000次．请你估计袋中红球接近（）

A、3 B、4 C、6 D、9

查看试题解析
6. 为了疫情防控，某小区需要从甲、乙、丙、丁4名志愿者中随机抽取2名负责该小区口处的测温工作，则甲被抽中的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{3}{4}$ D、 $\frac{5}{12}$

查看试题解析
7. 已知 $\frac{a}{2} = \frac{b}{3} = \frac{c}{4} \neq 0$ ，则 $\frac{a + b}{c}$ 的值为（）

A、 $\frac{5}{4}$ B、 $\frac{4}{5}$ C、2 D、 $\frac{1}{2}$

查看试题解析
8. 如图，在 $△ A B C$ 中， $D$ 是 $A B$ 边上一点，过点 $D$ 作 $D E / / B C$ 交 $A C$ 于点 $E$ ，若 $A D$ ： $D B = 3$ ： $1$ ，则 $S_{△ A D E}$ ： $S_{△ A B C}$ 的值为（）

A、 $\frac{3}{7}$ B、 $\frac{3}{4}$ C、 $\frac{16}{9}$ D、 $\frac{9}{16}$

查看试题解析
9. 如图，将矩形ABCD沿着GE，EC，GF翻折，使得点A，B，D恰好都落在点O处，且点G，O，C在同一条直线上，点E，O，F 在另一条直线上. 以下结论正确的是（）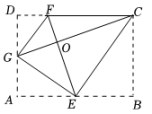

A、△COF∽△CEG B、OC=3OF C、AB：AD=4：3 D、GE= $\sqrt{6}$ DF

查看试题解析
10. 将2张相同的正方形纸片和2张相同的小长方形纸片按如图所示摆放在矩形ABCD内，中间留有一个小正方形未被覆盖.经过EF的直线交AD于点 $M$ ，交BC于点 $N$ ，若 $\frac{D M}{D G} = \frac{1}{2}$ ，则 $\frac{A B}{B C}$ 的值为（）

A、 $\frac{5}{7}$ B、 $\frac{3}{4}$ C、 $\frac{2}{3}$ D、 $\frac{7}{9}$

查看试题解析

二、填空题（每空3分，共15分）

11. 把方程 $x (x - 1) = x - 2$ 化成一元二次方程的一般形是.

查看试题解析
12. 观察表格，一元二次方程 $x^{2} - x - 1.1 = 0$ 的一个解的取值范围是．
x
1.3
1.4
1.5
1.6
1.7
1.8
1.9
$x^{2} - x - 1.1$
00.71
-0.54
-0.35
-0.14
0.09
0.34
0.61

查看试题解析
13. 如图，直线 $A D$ ， $B C$ 交于点 $O$ ， $A B / / E F / / C D$ ，若 $A O = 2$ ， $O F = 1$ ， $F D = 2$ ，则 $\frac{B E}{E C}$ 的值为．

查看试题解析
14. 如图，在矩形 $A B C D$ 中， $A B = 2.5$ ， $A D = 14$ ，点E在 $A D$ 上且 $D E = 2$ ．点G为 $A E$ 的中点，点P为 $B C$ 边上的一个动点，F为 $E P$ 的中点，则 $G F + E F$ 的最小值为．

查看试题解析
15. 四边形ABCD是正方形，点E是直线AD上的一点，连接CE（C、E、F、G四个点按照逆时针方向排序），直线BE与直线GD交于点H ，若AE＝2，则点F到GH的距离为．

查看试题解析

三、解答题（共7题，共55分）

16. 解下列方程

(1)、x²＋2x－4＝0

(2)、 $x^{2} - 3 \sqrt{2} x + 2 = 0$

(3)、2（x－3）²＝x²－9

查看试题解析
17. 已知关于x的方程x²－6x－m²＋3m＋5＝0．

(1)、试说明此方程总有两个不相等的实数根；

(2)、若此方程的一个根是－1，求另一根．

查看试题解析
18. 某中学运动队有短跑、长跑、跳远、实心球四个训练小队，现将四个训练小队队员情况绘制成如下不完整的统计图：

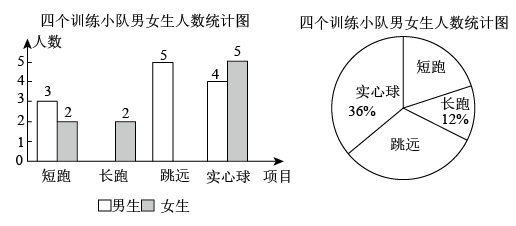(1)、学校运动队的队员总人数为；

(2)、补全条形统计图，并标明数据；

(3)、若在长跑训练小组中随机选取2名同学进行比赛，请用列举法（画树状图或列表）求所选取的这两名同学恰好是一男一女的概率.

查看试题解析
19. 如图，△ABC中，AB＝BC，过A点作BC的平行线与∠ABC的平分线交于点D，连接CD．

(1)、求证：四边形ABCD是菱形；

(2)、过点D作AC的平行线交直线BC于点E，连接DE，点P是线段BD上的动点，若 $A D = 5 ， A C = 2 \sqrt{5}$ ，请直接写出PC+PE的最小值．

查看试题解析
20. “人与自然和谐共生”哈尔滨湿地节系列活动中，某景点接待游客逐渐增多，6月份第一周接待游客200人，第三周接待游客288人，若该景点接待游客数量的周平均增长率相同.

(1)、求该景点在6月份的第二周接待游客多少人？

(2)、该景点第四周接待游客数量是第二周接待游客数量的1.8倍，平均每位游客购买1件旅游纪念品.该景点只销售A，B两种旅游纪念品，A种纪念品每件利润5元，B种纪念品每件利润8元，且售出的B种纪念品的数量不多于A种纪念品的3倍，设第四周该景点售出A种旅游纪念品a件，获得的总利润为W元，求W与a的函数关系式，并求出获得的最大利润.

查看试题解析
21. 如图1，点E是四边形 $A B C D$ 的边 $B C$ 上一点，分别连接 $E A$ ， $E D$ ，把四边形 $A B C D$ 分成三个三角形，如果其中有两个三角形相似，那么我们把点E叫做四边形 $A B C D$ 的边 $B C$ 上的“相似点”；如果这三个三角形都相似，那么我们把点E叫做四边形 $A B C D$ 的边 $B C$ 上的“强相似点”.

(1)、任务一：如图1， $∠ B = ∠ C = ∠ A E D = α °$ ，试判断点E是否是四边形 $A B C D$ 的边 $B C$ 上的“相似点”，并说明理由；

(2)、任务二：如图2，矩形 $A B C D$ 的四个顶点A，B，C，D均在正方形网格的格点上，试在图中画出矩形 $A B C D$ 的边 $B C$ 上的“强相似点”；

(3)、任务三：如图3，矩形 $A B C D$ 中， $A B = 6$ ，将矩形 $A B C D$ 沿 $C E$ 折叠，点D落在 $A B$ 边上的点F处，若点F是四边形 $A B C E$ 的边 $A B$ 上“强相似点”，求 $B C$ .

查看试题解析
22. 综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动.

(1)、操作判断
操作一：对折正方形纸片，使 $A D$ 与 $B C$ 重合，得到折痕 $E F$ ，把纸片展平；
操作二：在 $B E$ 上选一点 $H$ ，沿 $C H$ 折叠，使点 $B$ 落在 $E F$ 上的点 $G$ 处，得到折痕 $C H$ ，把纸片展平；根据以上操作，直接写出图1中 $∠ C H B$ 的度数：.

(2)、拓展应用
小华在以上操作的基础上，继续探究，延长 $H G$ 交 $A D$ 于点 $M$ ，连接 $C M$ 交 $E F$ 于点 $N$ （如图2）.判断 $△ M G N$ 的形状，并说明理由.

(3)、迁移探究
如图3，已知正方形 $A B C D$ 的边长为 $6 c m$ ，当点 $H$ 是边 $A B$ 的三等分点时，把 $△ B C H$ 沿 $C H$ 翻折得 $△ G C H$ ，延长 $H G$ 交 $A D$ 于点 $M$ ，请直接写出 $A M$ 的长.

查看试题解析

x	1.3	1.4	1.5	1.6	1.7	1.8	1.9
$x^{2} - x - 1.1$	00.71	-0.54	-0.35	-0.14	0.09	0.34	0.61