2023-2024学年浙教版数学七年级上学期期中仿真模拟试卷（三）

试卷更新日期：2023-10-23 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，共30分）

1. 若a与 $- 2$ 互为相反数，则a的倒数为（）

A、 $- 2$ B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
2. 妈妈的微信账单明细中+40元表示收入40元，那么﹣25元表示（）

A、收入25元 B、支出25元 C、收入15元 D、支出15元

查看试题解析
3. 在百度上搜索“疫情最新数据消息”，百度显示的相关结果约21800000个，将数据21800000用科学记数法表示为（）

A、2.18×10⁶ B、21.8×10⁶ C、2.18×10⁷ D、21.8×10⁷

查看试题解析
4. 下列说法中：（1）一个数，如果不是正数，必定就是负数；（2）整数与分数统称为有理数；（3）如果两个数的绝对值相等，那么这两个数相等；（4）符号不同的两个数互为相反数.其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 用 $- a$ 表示的数一定是（）

A、正数 B、负数 C、正数或负数 D、都不对

查看试题解析
6. 用代数式表示“ $a$ 的 $3$ 倍与 $b$ 的差的平方”，正确的是（）

A、 $3 （ a - b ）^{2}$ B、 $3 a - b^{2}$ C、 $（ a - 3 b ）^{2}$ D、 $（ 3 a - b ）^{2}$

查看试题解析
7. 如图， $a$ ， $b$ 是有理数，它们在数轴上的对应点的位置如图所示，把 $a$ ， $- a$ ， $b$ ， $- b$ 按照从大到小的顺序排列，正确的是（）

A、 $b > - a > a > - b$ B、 $b > a > - a > - b$ C、 $- a > b > a > - b$ D、 $- a > - b > a > b$

查看试题解析
8. 若 $（ x + 5 ）^{2} + | y - 2 | = 0$ ，则 $x + 2 y$ 的值为（）

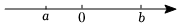A、 $9$ B、 $1$ C、 $- 1$ D、 $- 4$

查看试题解析
9. 下列合并同类项中，正确的是（　　）

A、 $2 x + 3 y = 5 x y$ B、 $3 x^{2} + 2 x^{3} = 5 x^{5}$ C、 $- 2 x^{2} + 2 x^{2} = x^{2}$ D、 $x^{2} - 3 x^{2} = - 2 x^{2}$

查看试题解析
10. 已知数a，b，c的大小关系如图，下列说法：①ab $+$ ac＞0；②﹣a﹣b $+$ c＞0；③ $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |} = 1$ ；④当x=0时，式子 $| x - b | + | x - c | + | x - a |$ 有最小值．其中正确结论的个数是（）

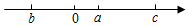A、1 B、2 C、3 D、4

查看试题解析

二、填空题（本大题共6小题，共24分）

11. 近似数2010.78万，精确到位

查看试题解析
12. 单项式 $- \frac{2}{3} a^{2} b^{3}$ 的系数是，多项式 $2 a^{2} b c^{3} - 3^{8} a c^{2} + 2^{10}$ 的次数是.

查看试题解析
13. 数轴上点A表示的数为5，则距离A点3个单位长度的点表示的数为.

查看试题解析
14. 若 $3^{4} = 3^{a}$ ， $3^{4} + 3^{4} + 3^{4} = 3^{b}$ ，则 $a + b =$ ．

查看试题解析
15. 已知 $x^{2} + 3 x + 5$ 的值为 $10$ ，则代数式 $3 x^{2} + 9 x + 12$ 的值为．

查看试题解析
16. 观察下列式子： $a_{1} = \frac{3}{1 \times 4} = \frac{1}{1} - \frac{1}{4}$ ； $a_{2} = \frac{3}{4 \times 7} = \frac{1}{4} - \frac{1}{7}$ ； $a_{3} = \frac{3}{7 \times 10} = \frac{1}{7} - \frac{1}{10}$ ； $a_{4} = \frac{3}{10 \times 13} = \frac{1}{10} - \frac{1}{13}$ ；…，按此规律，计算 $a_{1} + a_{2} + a_{3} + \dots + a_{2020} =$ .

查看试题解析

三、解答题（本大题共7小题，共66分）

17. 把下列各数填在相应的大括号里： $- \frac{4}{5}$ ， $- 7$ ， $- 1. \dot{2} \dot{3}$ ， $- 3.2$ ， $0$ ， $1 - π$ ， $1$ ， $- 2^{2}$ ， $- 1008$ ， $0.3030030003 \dots$ (相邻两个3之间依次多一个0），
非负整数集合：{                        …}；

分数集合：{                            …}；

无理数集合：{                            }.

查看试题解析
18. 计算：

(1)、 $- 1^{2021} + {(- 2)}^{3} \div (- 6) - 1 - | - 5 |$

(2)、 $(- \frac{5}{3} + \frac{7}{6} - \frac{3}{4}) \times (- 12)$

查看试题解析
19. 实数 $a$ 在数轴上的对应点 $A$ 的位置如图所示， $b = | a - \sqrt{2} | + | 3 - a |$ ．

(1)、求 $b$ 的值；

(2)、已知 $b + 2$ 的小数部分是 $m$ ， $8 - b$ 的小数部分是 $n$ ，求 $2 m + 2 n + 1$ 的平方根．

查看试题解析
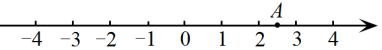20. 某市今年受台风“梅花”的影响，在抗洪抢险中，解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民，早晨从 $A$ 地出发，晚上到达 $B$ 地，约定向东为正方向，当天的航行路程记录如下 $（$ 单位：千米 $）$ ：
$+ 14$ ， $- 10$ ， $+ 8$ ， $- 7$ ， $+ 11$ ， $- 6$ ， $+ 9$ ， $- 5$ ．

(1)、请你帮忙确定 $B$ 地位于 $A$ 地的什么方向，距离 $A$ 地多少千米的地方？

(2)、若冲锋舟每千米耗油 $0.6$ 升，油箱容量为 $30$ 升，求冲锋舟当天救灾过程中至少还需补充多少升油？

查看试题解析
21. 已知 $2 a - 1$ 的平方根是 $\pm 3$ ， $b - 9$ 的立方根是 $2$ ， $c$ 是 $\sqrt{12}$ 的整数部分．

(1)、求 $a$ 、 $b$ 、 $c$ 的值；

(2)、若 $x$ 是 $\sqrt{12}$ 的小数部分，求 $x - \sqrt{12} + 12$ 的值．

查看试题解析
22. 【发现问题】数形结合是解决数学问题的一种重要的思想方法，借助图的直观性，可以帮助我们更容易理解数学问题．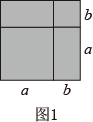
例如，求图1阴影部分的面积，可以得到乘法公式（a＋b）²＝a²＋2ab＋b²
请解答下列问题：

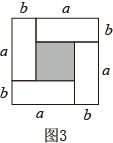
(1)、请写出求图2阴影部分的面积能解释的乘法公式（直接写出乘法公式即可）

(2)、用4个全等的、长和宽分别为a、b的长方形，拼摆成如图3的正方形，请你观察求图3中阴影部分的面积，蕴含的相等关系，写出三个代数式：（a＋b）²、（a－b）²、ab之间的等量关系式（直接写出等量关系式即可）

(3)、【自主探索】
小明用图4中x张边长为a的正方形，y张边长为b的正方形，z张宽为a，长为b的长方形纸片拼出一个面积为（3a＋2b）（2a＋3b）长方形，请在下面方框中画出图形，并计算x＋z＝

(4)、【拓展迁移】
事实上，通过计算几何图形的体积也可以表示一些代数恒等式，图5表示的是一个边长为a＋b的正方体，请你根据图5求正方体的体积，写出一个代数恒等式：

查看试题解析
23. 【阅读理解】
若A，B，C为数轴上三点，若点C到A的距离是点C到B的距离2倍，我们就称点C是[A，B]的“妙点”．例如，如图1，点A表示的数为-1，点B表示的数为2．表示1的点C到点A的距离是2，到点B的距离是1，那么点C是[A，B]的“妙点”.又如，表示0的点D到点A的距离是1，到点B的距离是2，那么点D就不是[A，B]的“妙点”，但点D是[B，A]的“妙点”．

【知识应用】

如图2，M、N为数轴上两点，点M所表示的数为-2，点N所表示的数为4．

(1)、数3(填“是”或“不是”）[M，N]的“妙点”，数2(填“是”或“不是”）[N，M]的“妙点”.

(2)、若数轴上有一点Q表示的数是x，且点Q是[N，M]的妙点，求x的值.

(3)、如图3，A、B为数轴上两点，点A所表示的数为-40，点B所表示的数为20．现有一只电子蚂蚁P从点B出发，以2个单位每秒的速度向左运动，到达点A停止．当t为何值时，点P，A和B中恰有一个点为其余两点的“妙点”？（请直接写出答案）

查看试题解析