2023-2024学年浙教版数学八年级(上)期中仿真模拟试卷(二)
试卷更新日期:2023-10-22 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 下列图标是节水、绿色食品、回收、节能的标志,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在中,画出边上的高( )A、
2. 如图,在中,画出边上的高( )A、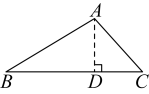 B、
B、 C、
C、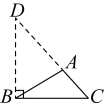 D、
D、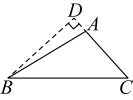 3. 已知 , 下列不等式的变形错误的是( )A、 B、 C、 D、4. 等腰三角形的两边长分别为和 , 则这个三角形的周长为( )A、 B、 C、 D、或5. 满足下列条件的△ABC中,不是直角三角形的是( )A、∠A=2∠B=3∠C B、∠B+∠A=∠C C、两个内角互余 D、∠A:∠B:∠C=2:3:56. 下列命题中,假命题是( )A、全等三角形对应角相等 B、对顶角相等 C、同位角相等 D、有两边对应相等的直角三角形全等7. 已知一个三角形的三条边长之比为3:4:5,且三角形的周长为24cm,则三角形的面积为( )A、 B、 C、 D、8. 如图,的三边、、的长分别是8、12、16,点O是三条角平分线的交点,则的值为( )
3. 已知 , 下列不等式的变形错误的是( )A、 B、 C、 D、4. 等腰三角形的两边长分别为和 , 则这个三角形的周长为( )A、 B、 C、 D、或5. 满足下列条件的△ABC中,不是直角三角形的是( )A、∠A=2∠B=3∠C B、∠B+∠A=∠C C、两个内角互余 D、∠A:∠B:∠C=2:3:56. 下列命题中,假命题是( )A、全等三角形对应角相等 B、对顶角相等 C、同位角相等 D、有两边对应相等的直角三角形全等7. 已知一个三角形的三条边长之比为3:4:5,且三角形的周长为24cm,则三角形的面积为( )A、 B、 C、 D、8. 如图,的三边、、的长分别是8、12、16,点O是三条角平分线的交点,则的值为( ) A、 B、 C、 D、9. 如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点P、Q,作直线PQ交AB于点D,连接AD,若△ABC的周长为15,AB=6,则△ADC的周长为( )
A、 B、 C、 D、9. 如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点P、Q,作直线PQ交AB于点D,连接AD,若△ABC的周长为15,AB=6,则△ADC的周长为( )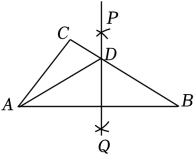 A、6 B、7 C、8 D、910. 如图,在和中, . 连接AC,BD交于点M,连接OM.则下列结论:①;②;③平分;④平分 . 其中正确结论的个数为( )
A、6 B、7 C、8 D、910. 如图,在和中, . 连接AC,BD交于点M,连接OM.则下列结论:①;②;③平分;④平分 . 其中正确结论的个数为( ) A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题(每空4分,共24分)
-
11. 根据“ 的2倍与3的差不小于8”列出的不等式是 .12. “若 , 则 , ”命题(选填“是”或“不是”).13. 三角形三个内角度数之比是1:2:3,则此三角形是三角形.14. 等腰中, , 顶角A为 , 平面内有一点P,满足且 , 则的度数为 .15. 如图,中, , , , , 平分 , 如果点P,点Q分别为 , 上的动点,那么的最小值是 .
 16. 图1是小馨在“天猫双12”活动中购买的一张多档位可调节靠椅.档位调节示意图如图2所示,已知两支脚米,米,为上固定连接点,靠背米.档位为Ⅰ档时, , 档位为Ⅱ档时,当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端向后靠的水平距离即为米.
16. 图1是小馨在“天猫双12”活动中购买的一张多档位可调节靠椅.档位调节示意图如图2所示,已知两支脚米,米,为上固定连接点,靠背米.档位为Ⅰ档时, , 档位为Ⅱ档时,当靠椅由Ⅰ档调节为Ⅱ档时,靠背顶端向后靠的水平距离即为米.
三、解答题(共8题,共66分)
-
17. 解不等式,并将解集在数轴上表示出来.(1)、;(2)、.18. 图①、图②、图③均是6×4的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,的顶点均在格点上,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上.


 (1)、在图①中以为边,画一个等腰;(2)、在图②中画 , 使与关于直线对称;(3)、在图③中画 , 使与全等.19. 如图,中,是的中线,是的角平分线,是的高.
(1)、在图①中以为边,画一个等腰;(2)、在图②中画 , 使与关于直线对称;(3)、在图③中画 , 使与全等.19. 如图,中,是的中线,是的角平分线,是的高.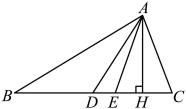 (1)、若的面积为8, , 求的长;(2)、若 , 求的度数.20. 如图 , 在平面直角坐标系中,点 , 连接 , 将绕点逆时针方向旋转到 .
(1)、若的面积为8, , 求的长;(2)、若 , 求的度数.20. 如图 , 在平面直角坐标系中,点 , 连接 , 将绕点逆时针方向旋转到 . (1)、求点的坐标;用字母 , 表示(2)、如图 , 延长交轴于点 , 过点作交轴于点 , 求证: .21. 如图,某人从A地到B地共有三条路可选,第一条路是从A到B,AB为10米,第二条路是从A经过C到达B地,AC为8米,BC为6米,第三条路是从A经过D地到B地共行走26米,若C、B、D刚好在一条直线上.
(1)、求点的坐标;用字母 , 表示(2)、如图 , 延长交轴于点 , 过点作交轴于点 , 求证: .21. 如图,某人从A地到B地共有三条路可选,第一条路是从A到B,AB为10米,第二条路是从A经过C到达B地,AC为8米,BC为6米,第三条路是从A经过D地到B地共行走26米,若C、B、D刚好在一条直线上. (1)、求证:;(2)、求AD和BD的长.22. 如图,在中,的垂直平分线交于点 , 交于点 , 于 , .
(1)、求证:;(2)、求AD和BD的长.22. 如图,在中,的垂直平分线交于点 , 交于点 , 于 , . (1)、求证:为线段的中点.(2)、若 , 求的度数.
(1)、求证:为线段的中点.(2)、若 , 求的度数.

