2023-2024学年浙教版数学八年级(上)期中仿真模拟试卷(一)
试卷更新日期:2023-10-22 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 下列四个图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 利用一块含角的透明直角三角板过点A作的边的垂线,下列三角板摆放的位置正确的是( )A、
2. 利用一块含角的透明直角三角板过点A作的边的垂线,下列三角板摆放的位置正确的是( )A、 B、
B、 C、
C、 D、
D、 3. 等腰三角形一边长为 , 一边长为 , 则它的周长等于( )A、16 B、17 C、16或17 D、以上都不对4. 下列长度的三条线段能组成三角形的是( )A、2,3,5 B、4,9,6 C、11,3,6 D、9,15,55. 下列说法中,正确结论的个数为( )
3. 等腰三角形一边长为 , 一边长为 , 则它的周长等于( )A、16 B、17 C、16或17 D、以上都不对4. 下列长度的三条线段能组成三角形的是( )A、2,3,5 B、4,9,6 C、11,3,6 D、9,15,55. 下列说法中,正确结论的个数为( )
(1)关于某一条直线对称的两个图形一定全等;
(2)有一角为 , 且腰长相等的两个等腰三角形全等;
(3)有一个外角是的等腰三角形是等边三角形;
(4)如果一个三角形的一个外角的角平分线与这个三角形的一边平行,那么这个三角形一定是等腰三角形.A、1个 B、2个 C、3个 D、4个6. 如下图,地面上有三个洞口A、B、C,老鼠可从任意一个洞口跑出,猫为能同时最省力地顾及到三个洞口,尽快抓住老鼠,应该蹲在( ) A、三条角平分线的交点 B、三条边的中线的交点 C、三条高的交点 D、三条边的垂直平分线的交点7. 如图,点E,点F在直线AC上,AE=CF,AD=CB,下列条件中不能判断△ADF≌△CBE的是( )
A、三条角平分线的交点 B、三条边的中线的交点 C、三条高的交点 D、三条边的垂直平分线的交点7. 如图,点E,点F在直线AC上,AE=CF,AD=CB,下列条件中不能判断△ADF≌△CBE的是( ) A、AD∥BC B、BE∥DF C、BE=DF D、∠A=∠C8. 如图,小逸家的房门左下角受潮了,他想检测房门是否变形,准备采用如下方法:先测量门的边AB和BC的长,再测量点A和点C间的距离,由此可推断是否为直角,这样做的依据是( )
A、AD∥BC B、BE∥DF C、BE=DF D、∠A=∠C8. 如图,小逸家的房门左下角受潮了,他想检测房门是否变形,准备采用如下方法:先测量门的边AB和BC的长,再测量点A和点C间的距离,由此可推断是否为直角,这样做的依据是( ) A、勾股定理 B、三角形内角和定理 C、勾股定理的逆定理 D、直角三角形的两锐角互余9. 在中,边 , 的垂直平分线、相交于点 , 若 , 则的度数是 . ( )
A、勾股定理 B、三角形内角和定理 C、勾股定理的逆定理 D、直角三角形的两锐角互余9. 在中,边 , 的垂直平分线、相交于点 , 若 , 则的度数是 . ( ) A、 B、 C、 D、10. 在学习勾股定理时,甲同学用四个相同的直角三角形直角边长分别为 , , 斜边长为构成如图所示的正方形;乙同学用边长分别为 , 的两个正方形和长为 , 宽为的两个长方形构成如图所示的正方形,甲、乙两位同学给出的构图方案,可以证明勾股定理的是( )
A、 B、 C、 D、10. 在学习勾股定理时,甲同学用四个相同的直角三角形直角边长分别为 , , 斜边长为构成如图所示的正方形;乙同学用边长分别为 , 的两个正方形和长为 , 宽为的两个长方形构成如图所示的正方形,甲、乙两位同学给出的构图方案,可以证明勾股定理的是( ) A、甲 B、乙 C、甲,乙都可以 D、甲,乙都不可以
A、甲 B、乙 C、甲,乙都可以 D、甲,乙都不可以二、填空题(每空4分,共24分)
-
11. 命题:直角三角形两条直角边的平方和等于斜边的平方,其逆命题是.12. 一个等腰三角形的两边长分别为 , , 则它的周长为 .13. 如图,点B、F、C、E在一条直线上, , , 若用“”判定 , 则添加的一个条件是 .
 14. 如图,在中, , , 分别以点和点为圆心,大于的长为半径画弧,两弧相交于点 , , 作直线 , 交于点 , 连接 , 则的度数为 .
14. 如图,在中, , , 分别以点和点为圆心,大于的长为半径画弧,两弧相交于点 , , 作直线 , 交于点 , 连接 , 则的度数为 .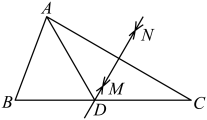 15. 如图, , 点在的角平分线上, , 点、是两边、上的动点,当的周长最小时,点到距离是.
15. 如图, , 点在的角平分线上, , 点、是两边、上的动点,当的周长最小时,点到距离是. 16. 如图,已知和都是等边三角形,点 在同一条直线上,交于M,交于N, 交点O;下列说法:①;②为等边三角形;③;④平分∠.其中一定正确的是(只需填写序号).
16. 如图,已知和都是等边三角形,点 在同一条直线上,交于M,交于N, 交点O;下列说法:①;②为等边三角形;③;④平分∠.其中一定正确的是(只需填写序号).
三、解答题(共7题,共66分)
-
17. 在如图所示的方格纸中,

⑴在中,作BC边上的高AD.
⑵作AC边上的中线BE.
⑶求的面积.
18. 如图中, , , D是边上一点,连接 , 垂足为点C,且 , 交线段于点F. (1)、在图1中画出正确的图形,并证明;(2)、当时,求证:平分 .19. 如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB .
(1)、在图1中画出正确的图形,并证明;(2)、当时,求证:平分 .19. 如图,在笔直的公路AB旁有一座山,为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处,已知点C与公路上的停靠站A的距离为15km,与公路上另一停靠站B的距离为20km,停靠站A、B之间的距离为25km,且CD⊥AB .
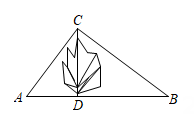
(1)、求修建的公路CD的长;(2)、若公路CD修通后,一辆货车从C处经过D点到B处的路程是多少?20. 如图,在△ABC中,∠B=40°,∠C=50°.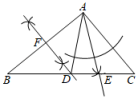 (1)、通过观察尺规作图的痕迹,可以发现直线DF是线段AB的 , 射线AE是∠DAC的 ;(2)、在(1)所作的图中,求∠DAE的度数.21. 等面积法是一种常用的、重要的数学解题方法.
(1)、通过观察尺规作图的痕迹,可以发现直线DF是线段AB的 , 射线AE是∠DAC的 ;(2)、在(1)所作的图中,求∠DAE的度数.21. 等面积法是一种常用的、重要的数学解题方法. (1)、如图1,在中, , , , , , 则的长为:.(2)、如图2,在中, , , 则的高与的比是: .(3)、如图3,在中, , 点D,P分别在边 , 上,且 , , , 垂足分别为点E,F.若 , 求的值.22. 在中, , 直线经过点C,且于D,于E.
(1)、如图1,在中, , , , , , 则的长为:.(2)、如图2,在中, , , 则的高与的比是: .(3)、如图3,在中, , 点D,P分别在边 , 上,且 , , , 垂足分别为点E,F.若 , 求的值.22. 在中, , 直线经过点C,且于D,于E. (1)、当直线绕点C旋转到图1的位置时,求证:
(1)、当直线绕点C旋转到图1的位置时,求证:①;
② .
(2)、当直线绕点C旋转到图2的位置时,求证:;(3)、当直线绕点C旋转到图3的位置时,试问具有怎样的等量关系?请写出这个等量关系,并加以证明.23. 概念学习规定:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“等角三角形”.
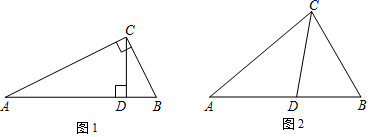
从三角形不是等腰三角形一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“等角三角形”,我们把这条线段叫做这个三角形的“等角分割线”.
 (1)、理解概念
(1)、理解概念
如图1,在中, , , 请写出图中两对“等角三角形”(2)、概念应用
如图2,在中,为角平分线, , .求证:为的等角分割线.
(3)、在中, , 是的等角分割线,直接写出的度数.