2023-2024学年浙教版数学七年级（上）期中仿真模拟试卷（二）

试卷更新日期：2023-10-22 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 2023的相反数为（）

A、-2023 B、 $- \frac{1}{2023}$ C、 $\frac{1}{2023}$ D、2023

查看试题解析
2. 单项式 $- 3 x^{3} y$ 的次数是（）

A、3 B、1 C、-3 D、4

查看试题解析
3. 2022年我国夏粮生产喜获丰收，为稳定全年粮食生产奠定了良好的基础，为稳物价保民生、稳定经济大盘、应对外部环境的不确定性提供了坚实的支撑．据统计，2022年全国夏粮播种面积397950000亩，比上年增长了0.3%，两年实现增长．将397950000用科学记数法表示应为（）

A、 $0.39795 \times 1 0^{9}$ B、 $39.795 \times 1 0^{7}$ C、 $3.9795 \times 1 0^{8}$ D、 $3.9795 \times 1 0^{7}$

查看试题解析
4. 下列说法中，错误的是（）

A、所有的有理数都可以用数轴上的点表示 B、数轴上的原点表示0 C、在数轴上表示-3的点与表示-1的点的距离是-2 D、数轴上表示-3的点在原点左边3个单位

查看试题解析
5. 下列说法中正确的是（）

A、0是最小的整数 B、1.30×10⁴精确到百分位 C、单项式 $\frac{2}{3} π x^{2}$ 的系数是 $\frac{2}{3}$ D、x³-2x²y²+3y²是四次三项式

查看试题解析
6. 关于 $\sqrt{8}$ 的叙述正确的是（）

A、在数轴上不存在表示 $\sqrt{8}$ 的点 B、 $\sqrt{8} = \sqrt{2} + \sqrt{6}$ C、 $\sqrt{8} = \pm \sqrt{2}$ D、与 $\sqrt{8}$ 最接近的整数是3

查看试题解析
7. 下列化简过程，正确的是（）

A、 $3 x + 3 y = 6 x y$ B、 $x + x = x^{2}$ C、 $- 9 y^{2} + 6 y^{2} = - 3$ D、 $- 6 x y^{2} + 6 y^{2} x = 0$

查看试题解析
8. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{5} = \sqrt{8}$ B、 $2 \sqrt{2} - \sqrt{2} = 1$ C、 $\sqrt[3]{8} = \pm 2$ D、 $\sqrt{0.36} = 0.6$

查看试题解析
9. 将连续的奇数1、3、5、7、…、，按一定规律排成如表：

图中的T字框框住了四个数字，若将T字框上下左右移动，按同样的方式可框住另外的四个数，若将T字框上下左右移动，则框住的四个数的和不可能得到的数是（）

A、22 B、70 C、182 D、206

查看试题解析
10. 如图，根据计算长方形 $ABCD$ 的面积，可以说明下列等式成立的是（）

A、 ${(a + b)}^{2} = a^{2} + 2 ab + b^{2}$ B、 ${(a - b)}^{2} = a^{2} - 2 ab + b^{2}$ C、 $(a + b) (a - b) = a^{2} - b^{2}$ D、 $a (a + b) = a^{2} + ab$

查看试题解析

二、填空题（每小题3分，共24分）

11. 如果向东走5m记作＋5m，那么向西走3m记作m.

查看试题解析
12. 在实数：1， $- \sqrt{4}$ ， $\sqrt[3]{9}$ ， $\frac{22}{7}$ ， $π$ ， $3.1313313331 \dots ($ 两个1之间一次多一个 $3)$ 中，无理数有个 $.$

查看试题解析
13. 若单项式 $x_{}^{m - 1} y_{}^{2}$ 与 $- 2 x_{}^{3} y_{}^{n}$ 的差是单项式，则 $m - n$ 的值是．

查看试题解析
14. 在数轴上，﹣2对应的点为A，点B与点A的距离为 $\sqrt{7}$ ，则点B表示的数为．

查看试题解析
15. 云南少数民族服饰以其精美的花纹和艳丽的色彩越来越受到追求独立与个性的设计师的喜爱．某民族服饰的花边均是由若干个平移形成的有规律的图案，如图，第①个图案由4个组成，第②个图案由7个组成，第③个图案由10个组成，…，按此规律排列下去，第 $n$ 个图案中的个数为．

查看试题解析
16. 已知轮船在静水中的速度为（a+b）千米/时，逆流速度为（2a-b）千米/时，则顺流速度为千米/时

查看试题解析
17. 已知|a|＝5，|b|＝3，若|a+b|＝a+b，则a+b＝．

查看试题解析
18. 如果一个两位数a的个位数字与十位数字都不是零，且互不相同，我们称这个两位数为“英华数”，定义新运算：将一个“英华数”的个位数字与十位数字对调，把这个新两位数与原两位数的和与11的商记 $ω (a)$ ，例如：a=13，对调个位数字与十位数字得到新两位数31，新两位数与原两位数的和，31+13=44，和与11的商44÷11=4，所以 $ω (13) = 4$ ．根据以上定义，回答下列问题：

(1)、计算： $ω （ 27 ）$ ．

(2)、若m，n都是“英华数”，且m+n=100，则 $ω (m) + ω (n) =$ ．

查看试题解析

三、解答题（共6题共46分）

19. 计算：

(1)、 $- 32 - (- 14) + 4$ ；

(2)、 $\frac{8}{15} \div (\frac{1}{3} - 1) \times 2 \frac{1}{2}$

(3)、 $37 - (\frac{7}{9} - \frac{1}{6}) \times {(- 6)}^{2}$

(4)、 $- 2^{2} \div (- 3) - \frac{1}{3} \times [4 - {(- 6)}^{2}]$

查看试题解析

20. 甲、乙两商场上半年经营情况如下（“+”表示盈利，“-”表示亏本，以百万为单位）

月份	一	二	三	四	五	六
甲商场	+0.8	+0.6	-0.4	-0.1	+0.1	+0.2
乙商场	+1.3	+1.5	-0.6	-0.1	+0.4	-0.1

(1)、三月份乙商场比甲商场多亏损多少元；

(2)、六月份甲商场比乙商场多盈利多少元；

(3)、甲、乙两商场上半年平均每月分别盈利或亏损多少元.

查看试题解析

21. 已知 $A = 3 a^{2} + b^{2} - 5 a b$ ， $B = 2 a b - 3 b^{2} + 4 a^{2}$ ，

(1)、化简： $- B + 2 A$ ；

(2)、当 $a = - \frac{1}{2}$ ， $b = 2$ 时，求 $- B + 2 A$ 的值.

查看试题解析
22. 点A，点B在数轴上的位置如图所示，若A，点B从目前的位置同时出发，沿数轴相向（A向右，B向左）作匀速运动，速度分别为1个单位长度/秒和2个单位长度/秒，运动时间为t．

(1)、当运动时间为3秒时，点A表示的数是，点B表示的数为．这时点A和点B相距个单位长度；

(2)、当运动时间为t．请你解决以下问题：
①当点A与点B重合时，求t的值；

②当t为何值时，A、B两点相距2个单位长度？

查看试题解析
23. 用边长20cm的正方形硬纸板做底面直径为6cm，高为10cm的圆柱体盒子（图1），每个盒子由1个长方形侧面和2个圆形底面组成，硬纸板以A，B两种方法裁剪（裁剪后边角料不再利用）
A方法：剪2个侧面（图2）；B方法：剪9个底面.

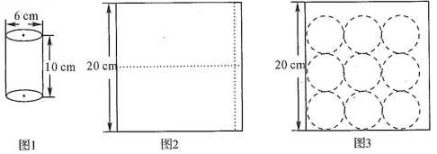(1)、请你计算A ，B 两种方法纸板的利用率（纸板利用率= $\frac{纸板被利用的面积}{纸板的总面积} \times 100 %$ ， $π$ 取3，结果精确到0.1%）；

(2)、现有26张硬纸板，裁剪时 $x$ 张用A方法，其余用B方法.
①用含 $x$ 的代数式分别表示裁剪出的侧面与底面的个数；
②若裁剪出的侧面和底面恰好全部用完，能做成多少个盒子？

查看试题解析
24. 某检修小组从A地出发，在东西方向的某路段上检修线路，若规定向东行驶的路程用正数表示，向西行驶的路程用负数表示，某一天该小组行驶的路程记录如下：（单位：km）＋10，－3，＋4，－2，－8，＋13，－7，＋12，＋7，＋5

(1)、问：收工时距A地多远？在A地的哪一侧？

(2)、在检修过程中，最远距离A处多远？在A地的哪一侧？

(3)、若该车每行驶1km耗油0.3升，问：这一天从出发到返回A地时共耗油多少升？

查看试题解析

2023-2024学年浙教版数学七年级（上）期中仿真模拟试卷（二）

一、选择题（每小题3分，共30分）

二、填空题（每小题3分，共24分）

三、解答题（共6题 共46分）

三、解答题（共6题共46分）