2023-2024学年浙教版数学九年级（上）期中仿真模拟试卷（二）

试卷更新日期：2023-10-22 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列函数中，是二次函数的是（）

A、y＝- $\frac{11}{x^{2}}$ B、y＝2x²-x+2 C、y＝ $\frac{1}{x}$ D、y＝2x+2

查看试题解析
2. 下列圆中既有圆心角又有圆周角的是（）．

A、 B、 C、 D、

查看试题解析
3. 某校生物兴趣小组为了解种子发芽情况，重复做了大量种子发芽的实验，结果如下：
实验种子的数量n
100
200
500
1000
5000
10000
发芽种子的数量m
98
182
485
900
4750
9500
种子发芽的频率 $\frac{m}{n}$
0.98
0.91
0.97
0.90
0.95
0.95
根据以上数据，估计该种子发芽的概率是（）

A、0.90 B、0.98 C、0.95 D、0.91

查看试题解析
4. 直角三角形的外心在（）

A、直角顶点 B、直角三角形内 C、直角三角形外 D、斜边中点

查看试题解析
5. 已知 $(- 4 ， y_{1})$ ， $(2.5 ， y_{2})$ ， $(5 ， y_{3})$ 是抛物线 $y = - 3 x^{2} - 6 x + m$ 上的点，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（）

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{3} > y_{2} > y_{1}$ C、 $y_{1} > y_{3} > y_{2}$ D、 $y_{2} > y_{1} > y_{3}$

查看试题解析
6. 已知二次函数y＝ax²＋bx＋c的x与y的部分对应值如下表：
x
…
－3
－2
－1
0
1
3
…
y
…
－27
－13
－3
3
5
－3
…
下列结论：①a＜0；②方程ax²＋bx＋c＝3的解为x₁＝0， x₂＝2；③当x＞2时，y＜0．
其中所有正确结论的序号是（）

A、①②③ B、① C、②③ D、①②

查看试题解析
7. 从甲，乙，丙三人中任选两名代表，甲被选中的可能性是（　　）

A、 $\frac{2}{3}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
8. 如图是一个圆柱形的玻璃水杯，将其横放，截面是个半径为 $5 c m$ 的圆，杯内水面 $A B = 8 c m$ ，则水深 $C D$ 是（）

A、 $\sqrt{2} c m$ B、 $\sqrt{3} c m$ C、 $2 c m$ D、 $3 c m$

查看试题解析
9. 已知点A，B，C在 $⊙ O$ 上， $∠ A B C = 30 °$ ，把劣弧 $\overset{⌢}{B C}$ 沿着直线 $C B$ 折叠交弦 $A B$ 于点D.若 $D B = 7$ ， $A D = 4$ ，则 $B C$ 的长为（）

A、 $5 \sqrt{3}$ B、9 C、 $6 \sqrt{3}$ D、 $7 \sqrt{3}$

查看试题解析
10. 如图1，校运动会上，初一的同学们进行了投实心球比赛．我们发现，实心球在空中飞行的轨迹可以近似看作是抛物线．如图2建立平面直角坐标系，已知实心球运动的高度y（m）与水平距离x（m）之间的函数关系是y= $- \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，则该同学此次投掷实心球的成绩是（）

A、2m B、6m C、8m D、10m

查看试题解析

二、填空题（每题4分，共24分）

11. 二次函数 $y = 2 {(x - 3)}^{2} + 1$ 的顶点坐标是.

查看试题解析
12. 线段 $O A$ 在平面直角坐标系内，A点坐标为 $(2 ， 5)$ ，线段 $O A$ 绕原点O逆时针旋转 $90 °$ ，得到线段 $O A^{^{'}}$ ，则点 $A^{'}$ 的坐标为.

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $∠ B = 36 °$ ，以 $C$ 为圆心， $C A$ 为半径的圆交 $A B$ 于点 $D$ ，交 $B C$ 于点 $E$ ．求弧 $D E$ 所对的圆心角的度数．

查看试题解析
14. 如图，直线 $y = k x + b$ 与抛物线 $y = - x^{2} + 2 x + 3$ 交于A，B两点，其中点A（0，3），点B（3，0），抛物线与x轴的另一交点C（－1，0），不等式－x²+2x+3>kx+b的解集为

查看试题解析
15. 任意投掷一枚正方体骰子（分别标有1，2，3，4，5，6），正面朝上是偶数的概率为．

查看试题解析
16. 如图，四边形 $A B C D$ 内接于 $⊙ O$ ，若它的一个外角 $∠ D C E = 68 °$ ，则 $∠ B O D =$ °．

查看试题解析

三、解答题（共8题，共66分）

17. 如图， $△ A B C$ 的三个顶点都在边长为1的小正方形组成的网格的格点上，以点 $O$ 为原点建立直角坐标系，回答下列问题：
⑴将 $△ A B C$ 先向上平移5个单位，再向右平移1个单位得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ ，并直接写出 $A_{1}$ 的坐标 ▲ ；
⑵将 $△ A_{1} B_{1} C_{1}$ 绕点 $(0 ， - 1)$ 顺时针旋转90°得到 $△ A_{2} B_{2} C_{2}$ ，画出 $△ A_{2} B_{2} C_{2}$ ；
⑶观察图形发现， $△ A_{2} B_{2} C_{2}$ 是由 $△ A B C$ 绕点 ▲ （写出点的坐标）顺时针旋转 ▲ 度得到的.

查看试题解析
18. 如图， $A B$ 是 $⊙ O$ 直径，弦 $C D ⊥ A B$ 于点E，过点C作 $D B$ 的垂线，交 $A B$ 的延长线于点G，垂足为点F，连结 $A C$ ，其中 $∠ A = ∠ D$ ．

(1)、求证： $A C = C G$ ；

(2)、若 $C D = E G = 8$ ，求 $⊙ O$ 的半径．

查看试题解析
19.

(1)、如图所示分别是二次函数 $y = a x^{2} + b x + c$ 与 $y = a^{'} x^{2} + b^{'} x + c^{'}$ 的图象.用“ $<$ ”或“ $>$ ”填空： $a$ $a^{'}$ ， $c$ $c^{'}$ .

(2)、在本学期我们已经学习了一元二次方程的三种解法，他们分别是配方法、公式法和因式分解法，请从下列一元二次方程中任选两个，并解这两个方程.
① $(x - 3)^{2} = 5 (3 - x)$ ；
② $(2 x - 1)^{2} - 9 = 0$ ；
③ $2 x^{2} - \sqrt{3} x - 3 = 0$ ；
④ $x^{2} - 2 x - 15 = 0$ .

查看试题解析
20. 今年以来，某市接待游客人数逐月增加，据统计，八月份和十月份到某景区游玩的游客人数分别为4万人和5.76万人．

(1)、求八月到十月该景区游客人数平均每月的增长率；

(2)、若该景区仅有A，B两个景点，售票处出示的三种购票方式如表所示：
购票方式
甲
乙
丙
可游玩景点
A
B
A和B
门票价格
100元/人
80元/人
160元/人
据预测，十一月份选择甲、乙、丙三种购票方式的人数分别有2万人、3万人和2万人，并且当甲、乙两种门票价格不变时，丙种门票价格每下降1元，将有600名原计划购买甲种门票的游客和400名原计划购买乙种门票的游客改为购买丙种门票．设十一月份景区门票总收入为W万元，丙种门票下降m元，请写出W与m之间的表达式，并求出要想让十一月份门票总收入达到798万元，丙种门票应该下降多少元？

查看试题解析
21. 如图所示为某商场的一个可以自由转动的转盘，商场规定顾客购物满100元即可获得一次转动转盘的机会，当转盘停止时，指针落在哪一个区域就获得相应的奖品，如表是活动进行中的统计数据：
转动转盘的次数
50
100
200
500
800
1000
2000
5000
落在“纸巾”区的次数
22
71
109
312
473
612
1193
3004
根据以上信息，解析下列问题：

(1)、请估计转动该转盘一次，获得纸巾的概率是；（精确到0.1）

(2)、现有若干个除颜色外都相同的白球和黑球，根据（1）的结论，在保证获得纸巾和免洗洗手液概率不变的情况下，请你设计一个可行的摸球抽奖规则，详细说明步骤；

(3)、小明和小亮都购买了超过100元的商品，均获得一次转动转盘的机会，根据（2）中设计的规则，利用画树状图或列表的方法求两人都获得纸巾的概率．

查看试题解析
22. 如图，在平面直角坐标系中，O为原点，A（3，0），B（-3，0），D是y轴上的一个动点，∠ADC＝90°（A、D、C按顺时针方向排列），BC与经过A、B、D三点的OM交于点E，DE平分∠ADC，连结AE，BD。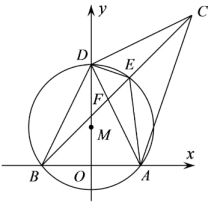

(1)、求证：∠ABC＝45°；

(2)、求证：∠DEC＝DEA；

(3)、若点D的坐标为（0，9），求AE的长．

查看试题解析
23. 若任意两个正数的和为定值，则它们的乘积会如何变化呢？会不会存在最大值？
特例研究：若两个正数的和是1，那么这两个正数可以是： $\frac{1}{2}$ 和 $\frac{1}{2}$ ， $\frac{1}{4}$ 和 $\frac{3}{4}$ ， $\frac{1}{5}$ 和 $\frac{4}{5}$ ， …

由于这样的正数有很多，我们不妨设其中一个正数是 $x$ ，另外一个正数为 $y$ ，那么 $x + y = 1$ ，则 $y = 1 - x$ ，所以 $z = x y = x (1 - x) = - x^{2} + x$ ， $0 < x < 1$ ，可以看出两数的乘积 $z$ 是 $x$ 的二次函数，乘积的最大值转化为求关于 $x$ 的二次函数的最值问题．

方法迁移：

(1)、若两个正数x和y的和是6，其中一个正数为 $x (0 < x < 6)$ ，这两个正数的乘积为z，写出z与x的函数关系式，并画出函数图象．

(2)、在（1）的条件下，z的最大值为：，并写出此时函数图象的至少一个性质．

(3)、问题解决：
由以上题目可知若任意两个正数的和是一个固定的数，那么这两个正数的乘积存在最大值，即对于正数x，y，若x+y是定值，则xy存在最大值．

类比应用：

利用上面所得到的结论，完成填空：

①已知函数 $y_{1} = 2 x - 2 (x > 1)$ 与函数 $y_{2} = - 2 x + 8 (x < 4)$ ，则当x＝时， $y_{1} • y_{2}$ 取得最大值为；

②已知函数y₁＝2x-2+m（x≥1），m为正定值，函数y₂＝-2x+8（x<4），则当x为何值时， $y_{1} • y_{2}$ 取得最大值，最大值是多少？

查看试题解析
24. 已知抛物线y=x²+bx+c的图象如图所示，它与x轴的一个交点的坐标为A（-1，0），与y轴的交点坐标为C（0，3） .

(1)、求抛物线的解析式及与x轴的另一个交点B的坐标；

(2)、根据图象回答：当x取何值时，y＜0？

(3)、在抛物线的对称轴上有一动点P，求 $PA + PC$ 的值最小时的点P的坐标．

查看试题解析

实验种子的数量n	100	200	500	1000	5000	10000
发芽种子的数量m	98	182	485	900	4750	9500
种子发芽的频率 $\frac{m}{n}$	0.98	0.91	0.97	0.90	0.95	0.95

购票方式	甲	乙	丙
可游玩景点	A	B	A和B
门票价格	100元/人	80元/人	160元/人

转动转盘的次数	50	100	200	500	800	1000	2000	5000
落在“纸巾”区的次数	22	71	109	312	473	612	1193	3004

x	…	－3	－2	－1	0	1	3	…
y	…	－27	－13	－3	3	5	－3	…