2023-2024学年浙教版数学九年级（上）期中仿真模拟试卷（一）

试卷更新日期：2023-10-22 类型：期中考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 在同一平面内，已知 $⊙ O$ 的半径为2，圆心O到直线l的距离为3，点P为圆上的一个动点，则点P到直线l的最大距离是（）

A、2 B、5 C、6 D、8

查看试题解析
2. 下列事件为必然事件的是（）

A、车辆随机经过一个路口，遇到红灯 B、6月份海南气温达到零下20度 C、射箭射中十环 D、画一个四边形，其内角和为 $360 °$

查看试题解析
3. 将抛物线 $y = x^{2}$ 向上平移 $5$ 个单位长度，得到的抛物线的解析式为（）

A、 $y = (x + 5)^{2}$ B、 $y = (x - 5)^{2}$ C、 $y = x^{2} + 5$ D、 $y = x^{2} - 5$

查看试题解析
4. 已知二次函数y＝a（x-k）（x+k-6），当x＝x₁时，函数值为y₁ ，当x＝x₂时，函数值为y₂ ，若|x₁-3|＜|x₂-3|，则下列结论正确的是（）

A、y₁-y₂＜0 B、a（y₁-y₂）＜0 C、y₁+y₂＞0 D、a（y₁+y₂）＞0

查看试题解析
5. 如图， $A B$ ， $B C$ 为 $⊙ O$ 的两条弦，连结 $O A$ ， $O C$ ，点 $D$ 为 $A B$ 的延长线上一点．若 $∠ C B D = 65 °$ ，则 $∠ A O C$ 为（）

A、 $110 °$ B、 $115 °$ C、 $125 °$ D、 $130 °$

查看试题解析
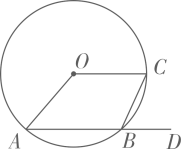6. 如图，⊙O的直径CD垂直弦AB于点E，且CE=2， DE=8，则AB的长为（）

A、4 B、6 C、7 D、8

查看试题解析
7. 若二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，则不等式 $a {(x - 2)}^{2} + b (x - 2) + c < 0$ 的解集为（　　）

A、 $x < 1$ 或 $x > 3$ B、 $x > 3$ C、 $x < - 1$ D、 $x < 3$ 或 $x > 5$

查看试题解析
8. 二次函数y＝ax²＋bx＋c的图象如图所示，则函数y＝bx＋c的图象和函数y＝ $\frac{a + b + c}{x}$ 的图象在同一坐标系中大致为（）

A、 B、 C、 D、

查看试题解析
9. 如图， $A B$ 是 $⊙ O$ 的直径，点 $C$ 、 $D$ 在圆周上， $∠ C A B = 30 °$ ，则 $∠ A D C$ 的度数为（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $75 °$

查看试题解析
10. 已知y关于x的二次函数 $y = 2 m x^{2} + (1 - m) x - 1 - m$ ，下列结论中正确的序号是（）
①当 $m = - 1$ 时，函数图象的顶点坐标为 $(\frac{1}{2} ， \frac{1}{2})$ ；②当m≠0时，函数图象总过定点：③当 $m > 0$ 时，函数图象在x轴上截得的线段的长度大于 $\frac{3}{2}$ ；④若函数图象上任取不同的两点 $P_{1} (x_{1} ， y_{1})$ 、 $P_{2} (x_{2} ， y_{2})$ ，则当 $m < 0$ 时，函数在 $x > \frac{1}{4}$ 时一定能使 $\frac{y_{2} - y_{1}}{x_{2} - x_{1}} < 0$ 成立．

A、①②③ B、①③④ C、②③④ D、①②④

查看试题解析

二、填空题（每题4分，共24分）

11. 如图，四边形 $A B C D$ 内接于圆 $O$ ，若 $∠ D = 10 0^{°}$ ，则 $∠ B$ 的度数是.

查看试题解析
12. 如图， $△ A B C$ 中， $A C = B C$ ，圆O是 $△ A B C$ 的外接圆， $B O$ 的延长线交边 $A C$ 于点D.当 $△ A B D$ 是等腰三角形时， $∠ A$ 的度数为.

查看试题解析
13. 如图是郑州圆形“戒指桥”，其数学模型为如图所示.已知桥面跨径AB＝20米，D为圆上一点，DC⊥AB于点C，且CD＝BC＝14米，则该圆的半径长为米.

查看试题解析
14. 衢州飞往成都每天有2趟航班.小赵和小黄同一天从衢州飞往成都，如果他们可以选择其中任一航班，则他们选择同一航班的概率等于.

查看试题解析
15. 如图，一位运动员投篮，球沿y=-0.2x² +x+ 2.25抛物线运行，然后准确落入篮筐内，已知篮筐的中心离地面的高度为3.05m，则他距篮筐中心的水平距离OH是m.

查看试题解析
16. 如图，在正方形ABCD中，AB＝2 $\sqrt{2}$ ，将线段CD绕点C顺时针旋转α至射线l，作点D关于射线l的对称点M，连接BM交直线l于点N，当α＝°时，线段AN取得最大值；线段AN的最大值为.

查看试题解析

三、解答题（共7题，共66分）

17. 设二次函数

y = a x^{2} + b x - 3 (a ， b

是常数，

a \neq 0)

，部分对应值如表：

$x$	$\dots$	-2	-1	0	1	2	$\dots$
$y$	$\dots$	5	0	-3	-4	-3	$\dots$

(1)、试判断该函数图象的开口方向．

(2)、根据你的解题经验，直接写出

a x^{2} + b x - 3 = 0

的解．

(3)、当

x = 4

时，求函数

y

的值．

查看试题解析

18. 一个布袋中有8个红球和16个白球，它们除颜色外都相同．

(1)、求从袋中摸出一个球是红球的概率；

(2)、现从袋中取走若干个白球，并放入相同数量的红球．搅拌均匀后，要使从袋中摸出一个球是红球的概率是 $\frac{5}{8}$ ，问取走了多少个白球？（要求通过列式或列方程解答）

查看试题解析
19. 如图，在 $△ A B C$ 中，以边 $A B$ 为直径作 $⊙ O$ 分别交 $B C$ ， $A C$ 于点D，E，点D是 $B C$ 中点，连接 $O E$ ， $O D$ .

(1)、求证： $△ A B C$ 是等腰三角形.

(2)、若 $A B = 6$ ， $∠ A = 40 °$ ，求 $\overset{⌢}{A E}$ 的长和扇形 $E O D$ 的面积.

查看试题解析
20. 如图，在△ABC中，AB＝AC，以AB为直径的半圆O分别交BC，AC于点D，E，连接DE，OD．

(1)、求证： $\overset{⌢}{B D} = \overset{⌢}{E D}$ ．

(2)、当 $\overset{⌢}{A E}$ ， $\overset{⌢}{B E}$ 的度数之比为4∶5时，求四边形ABDE四个内角的度数．

查看试题解析
21. 如图1，点O为直线AB上一点，过点O作射线OC，使∠AOC＝60°．将一把直角三角尺的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方，其中∠OMN＝30°．

(1)、将图1中的三角尺绕点O顺时针旋转至图2，使一边OM在∠BOC的内部，且恰好平分∠BOC，求∠CON的度数；

(2)、将图1中的三角尺绕点O按每秒6°的速度绕点O沿顺时针方向旋转一周，OC也以每秒1°的速度绕点O顺时针方向旋转，当三角尺停止运动时，OC也停止运动．
①在旋转的过程中，问运动几秒时，边MN恰好与射线OC平行；
②将图1中的三角尺绕点O顺时针旋转至图3，使ON在∠AOC的内部，请探究∠AOM与∠NOC之间的数量关系（直接写出结果）．

查看试题解析

22. 根据以下素材，探索完成任务．

如何设计跳长绳方案
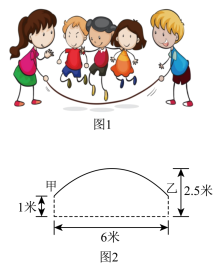
素材1	图1是集体跳长绳比赛，比赛时，各队跳绳10人，摇绳2人，共计12人．图2是绳甩到最高处时的示意图，可以近似的看作一条抛物线，正在甩绳的甲、乙两位队员拿绳的手间距6米，到地面的距离均为1米，绳子最高点距离地面2.5米．
素材2	某队跳绳成员有6名男生和4名女生，男生身高1.70米至1.80米，女生身高1.66米至1.68米．跳长绳比赛时，可以采用一路纵队或两路纵队并排的方式安排队员位置，但为了保证安全，人与人之间距离至少0.5米．
问题解决
任务1	确定长绳形状	在图2中建立合适的直角坐标系，并求出抛物线的函数表达式．
任务2	探究站队方式	当该队以一路纵队的方式跳绳时，绳子能否顺利的甩过所有队员的头顶？
任务3	拟定位置方案	为了更顺利的完成跳绳，现按中间高两边低的方式居中安排站位．请在你所建立的坐标系中，求出左边第一位跳绳队员横坐标的最大取值范围．

查看试题解析

23. 【概念引入】 $]$
在一个圆中，圆心到该圆的任意一条弦的距离，叫做这条弦的弦心距.

(1)、【概念理解】
如图1，在 $⊙ O$ 中，半径是5，弦 $A B = 8$ ，则这条弦的弦心距 $O C$ 长为.

(2)、通过大量的做题探究；小明发现：在同一个圆中，如果两条弦相等，那么这两条弦的弦心距也相等.但是小明想证明时却遇到了麻烦.请结合图2帮助小明完成证明过程如图2，在 $⊙ O$ 中， $A B = C D$ ， $O M ⊥ A B$ ， $O N ⊥ C D$ ，求证： $O M = O N$ .

(3)、【概念应用】
如图3，在 $⊙ O$ 中 $A B = C D = 16$ ， $⊙ O$ 的直径为20，且弦 $A B$ 垂直于弦 $C D$ 于 $E$ ，请应用上面得出的结论求 $O E$ 的长.

查看试题解析