【每日15min】17点与圆的位置关系—浙教版数学九(上)微专题复习
试卷更新日期:2023-10-22 类型:复习试卷
一、选择题
-
1. 在Rt△ABC中,∠ACB=90°,AC=6,AB=10,以C为圆心,BC为半径作⊙C,则点A与⊙C的位置关系是( )A、点A在⊙C内 B、点A在⊙C上 C、点A在⊙C外 D、无法确定2. 如图,在中, , , , 点D在边上, , 以点D为圆心作 , 其半径长为r,要使点A恰在外,点B在内,则r的取值范围是( )
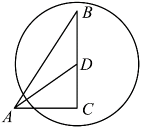 A、 B、 C、 D、3. 已知圆的半径为5cm,同一平面内一点到圆心的距离是6cm,则这点在( )A、圆外 B、圆上 C、圆内 D、不能确定4. 点到圆的距离为6,若点在圆外,则圆的半径满足( )A、 B、 C、 D、5. 如图,在中, , , .以点A为圆心,r为半径作圆,当点C在内且点B在外时,r的值可能是( )
A、 B、 C、 D、3. 已知圆的半径为5cm,同一平面内一点到圆心的距离是6cm,则这点在( )A、圆外 B、圆上 C、圆内 D、不能确定4. 点到圆的距离为6,若点在圆外,则圆的半径满足( )A、 B、 C、 D、5. 如图,在中, , , .以点A为圆心,r为半径作圆,当点C在内且点B在外时,r的值可能是( )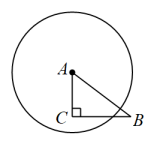 A、3 B、4 C、5 D、66. 如图,已知正方形 , 以点为圆心,长为半径作 , 点与的位置关系为( )
A、3 B、4 C、5 D、66. 如图,已知正方形 , 以点为圆心,长为半径作 , 点与的位置关系为( )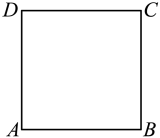 A、点在外 B、点在内 C、点在上 D、无法确定7. 如图,四边形为矩形, , .点P是线段上一动点,点M为线段上一点. , 则的最小值为( )
A、点在外 B、点在内 C、点在上 D、无法确定7. 如图,四边形为矩形, , .点P是线段上一动点,点M为线段上一点. , 则的最小值为( ) A、 B、 C、 D、8. 已知P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x,y都是整数,则这样的点共有( )A、4个 B、8个 C、12个 D、16个
A、 B、 C、 D、8. 已知P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x,y都是整数,则这样的点共有( )A、4个 B、8个 C、12个 D、16个二、填空题
-
9. 的半径是 , 点P与圆心O的距离是 , 则点在.(填写“内”、“上”、“外”)10. 一个点到圆上的点的最小距离为6cm , 最大距离为10cm , 则圆的半径为cm .11. 如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,使点A在⊙D内且点C在⊙D外,则r的取值范围是 .
 12. 如图,⊙M的半径为4,圆心M的坐标为(5,12),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为.
12. 如图,⊙M的半径为4,圆心M的坐标为(5,12),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为.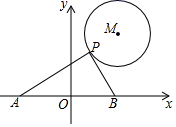
三、综合题
-
13. 圆圆在解答问题“在矩形中,以A为圆心作 , 使得B,C,D三点中至少有一点在内,有一点在外,求的半径r的取值范围?”时,答案为“”.圆圆的答案对吗?如果错误,请写出正确的解答过程.
 14. 如图,在矩形ABCD中,AB=6cm,AD=8cm,
14. 如图,在矩形ABCD中,AB=6cm,AD=8cm, (1)、若以A为圆心,6cm长为半径作⊙A(画图),则B、C、D与圆的位置关系是什么?(2)、若作⊙A,使B、C、D三点至少有一个点在⊙A内,至少有一点在⊙A外,则⊙A的半径r的取值范围是 .15. 在平面直角坐标系中,有图形和点 , 我们规定:若图形上存在点、点和可以重合 , 满足 , 其中点是点关于轴的对称点,则称点是图形的“对称平衡点”.
(1)、若以A为圆心,6cm长为半径作⊙A(画图),则B、C、D与圆的位置关系是什么?(2)、若作⊙A,使B、C、D三点至少有一个点在⊙A内,至少有一点在⊙A外,则⊙A的半径r的取值范围是 .15. 在平面直角坐标系中,有图形和点 , 我们规定:若图形上存在点、点和可以重合 , 满足 , 其中点是点关于轴的对称点,则称点是图形的“对称平衡点”. (1)、如图所示,已知,点 , 点 .
(1)、如图所示,已知,点 , 点 .
在点 , , 中,是线段的“对称平衡点”的是 ▲ ;
线段上是否存在线段的“对称平衡点”?若存在,请求出符合要求的“对称平衡点”的横坐标的范围,若不存在,请说明理由.(2)、如图 , 以点为圆心,为半径作坐标系内的点满足 , 再以点为圆心,为半径作 , 若上存在的“对称平衡点”,直接写出点纵坐标的取值范围.