【每日15min】21 一元一次不等式组—浙教版数学八(上)微专题精炼
试卷更新日期:2023-10-22 类型:复习试卷
一、选择题
-
1. 下列属于一元一次不等式组的是( )A、 B、 C、 D、2. 两个不等式的解集在数轴上表示如图,则这两个不等式组成的不等式组的解集是( )
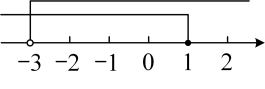 A、或 B、 C、 D、3. 不等式组的解在数轴上表示正确的是( )A、
A、或 B、 C、 D、3. 不等式组的解在数轴上表示正确的是( )A、 B、
B、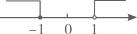 C、
C、 D、
D、 4. 已知关于x和y的方程组(k为常数),得到下列结论:
4. 已知关于x和y的方程组(k为常数),得到下列结论:①无论k取何值,都有4x+y=5;
②若k=1,则(2x-1)y=1;
③方程组有非负整数解时,k=1;
④若x和y互为相反数,则k= , 其中正确的个数为( )
A、1个 B、2个 C、3个 D、4个5. 若不等式组的解集为1<x<2,则(m+n)2022的值为( )A、-1 B、0 C、1 D、26. 关于x的不等式组 恰好只有两个整数解,则a的取值范围为( ).
A、5≤a<6 B、5<a≤6 C、4≤a<6 D、4<a≤67. 对于任意实数p、q,定义一种运算:p@q=p-q+pq,例如2@3=2-3+2×3.请根据上述定义解决问题:若关于x的不等式组有3个整数解,则m的取值范围为是 ( )A、-8≤m<-5 B、-8<m≤-5 C、-8≤m≤-5 D、-8<m<-58. 如图是测量一颗玻璃球体积的过程:
(1)将的水倒进一个容量为的杯子中;
(2)将五颗相同的玻璃球放入水中,结果水没有满;
(3)再加一颗同样的玻璃球放入水中,结果水满溢出.根据以上过程,推测这样一颗玻璃球的体积范围是( )
A、以上,以下 B、以上,以下 C、以上,以下 D、以上,以下9. 某商店甲商品的单价为8元,乙商品的单价为2元.已知购买乙商品的件数比购买甲商品的件数的2倍少4件,如果购买甲、乙两种商品的总件数不少于32,且购买甲、乙两种商品的总费用不超过148元.设购买甲商品x件,依题意可列不等式组得( )A、 B、 C、 D、二、填空题
-
10. 如图是不等式组的解在数轴上的表示,则此不等式组的整数解是.
 11. 已知 , 在关于 , 的二元一次方程组中, , , 则的取值范围是 , .12. 若关于x的不等式组的整数解为1,2,3,求适合条件的有序整数对的个数 .13. 运行程序如图所示,规定:从“输入一个值”到“结果是否”为一次程序操作,如果程序操作进行了三次才停止,那么的取值范围是.
11. 已知 , 在关于 , 的二元一次方程组中, , , 则的取值范围是 , .12. 若关于x的不等式组的整数解为1,2,3,求适合条件的有序整数对的个数 .13. 运行程序如图所示,规定:从“输入一个值”到“结果是否”为一次程序操作,如果程序操作进行了三次才停止,那么的取值范围是.
三、解答题
-
14.(1)、解不等式: , 并把解集在数轴上表示出来;
 (2)、解不等式组 , 并写出它的最大整数解.15. 以下是圆圆解不等式组的解答过程:
(2)、解不等式组 , 并写出它的最大整数解.15. 以下是圆圆解不等式组的解答过程:解:由①,得 , 所以 .
由②,得 , 所以 ,
所以 . 所以原不等式组的解是 .
圆圆的解答过程是否有错误?如果有错误,请写出正确的解答过程.
16. 为更好地推进生活垃圾分类工作,改善城市生态环境,某小区准备购买A、B两种型号的垃圾箱,通过对市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需390元,购买2个A型垃圾箱比购买1个B型垃圾箱少用20元.(1)、求每个A型垃圾箱和每个B型垃圾箱分别多少元?(2)、该小区计划用不多于1500元的资金购买A、B两种型号的垃圾箱共20个,且A型号垃圾箱个数不多于B型垃圾箱个数的3倍,则该小区购买A、B两种型号垃圾箱的方案有哪些?