【每日15min】17 勾股定理—浙教版数学八(上)微专题复习
试卷更新日期:2023-10-22 类型:复习试卷
一、选择题
-
1. 下列各组3个整数是勾股数的是( )A、4,5,6 B、6,8,9 C、13,14,15 D、8,15,172. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,那么小巷的宽度为( )
 A、0.7米 B、1.5米 C、2.2米 D、2.4米3. 如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,则线段GH的长为( )
A、0.7米 B、1.5米 C、2.2米 D、2.4米3. 如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,则线段GH的长为( )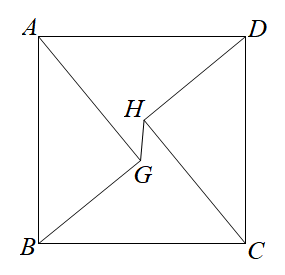 A、 B、 C、 D、4. 意大利文艺复兴时期的著名画家达•芬奇利用两张一样的纸片拼出不一样的“空洞”,从而巧妙的证明了勾股定理.小明用两张全等的的纸片①和②拼成如图1所示的图形,中间的六边形 由两个正方形和两个全等的直角三角形组成.已知六边形 的面积为28, .小明将纸片②翻转后拼成如图2所示的图形,其中 ,则四边形 的面积为( )
A、 B、 C、 D、4. 意大利文艺复兴时期的著名画家达•芬奇利用两张一样的纸片拼出不一样的“空洞”,从而巧妙的证明了勾股定理.小明用两张全等的的纸片①和②拼成如图1所示的图形,中间的六边形 由两个正方形和两个全等的直角三角形组成.已知六边形 的面积为28, .小明将纸片②翻转后拼成如图2所示的图形,其中 ,则四边形 的面积为( )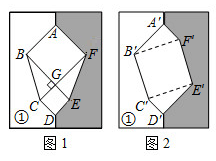 A、16 B、20 C、22 D、245. 以下列各组数为边长,能构成直角三角形的是( )A、 , , 2 B、1,2, C、1, , D、4,5,66. 数形结合是数学的重要思想和解题方法,如:“当0<x<12时,求代数式 的最小值”,其中 可看作两直角边分别为x和2的Rt△ACP的斜边长, 可看作两直角边分别是12-x和3的Rt△BDP的斜边长.于是将问题转化为求AP+BP的最小值,如图所示,当AP与BP共线时,AP+BP为最小.请你解决问题:当0<x<4时,则代数式 的最小值是( )
A、16 B、20 C、22 D、245. 以下列各组数为边长,能构成直角三角形的是( )A、 , , 2 B、1,2, C、1, , D、4,5,66. 数形结合是数学的重要思想和解题方法,如:“当0<x<12时,求代数式 的最小值”,其中 可看作两直角边分别为x和2的Rt△ACP的斜边长, 可看作两直角边分别是12-x和3的Rt△BDP的斜边长.于是将问题转化为求AP+BP的最小值,如图所示,当AP与BP共线时,AP+BP为最小.请你解决问题:当0<x<4时,则代数式 的最小值是( ) A、4 B、5 C、6 D、77. 如图所示,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( )
A、4 B、5 C、6 D、77. 如图所示,已知△ABC中,AB=6,AC=9,AD⊥BC于D,M为AD上任一点,则MC2-MB2等于( ) A、9 B、35 C、45 D、无法计算8. 如图,在底面半径为2,(π取3)高为8的圆柱体上有只小虫子在A点,它想爬到B点,则爬行的最短路程是( )
A、9 B、35 C、45 D、无法计算8. 如图,在底面半径为2,(π取3)高为8的圆柱体上有只小虫子在A点,它想爬到B点,则爬行的最短路程是( ) A、10 B、8 C、5 D、4
A、10 B、8 C、5 D、4二、填空题
-
9. 已知两边长为5和12,则其斜边上的中线为.10. 如图是一个滑梯示意图,左边是楼梯,右边是滑道,已知滑道与的长度相等,滑梯的高度 , .则滑道的长度为m.
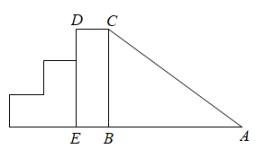 11. 如图所示的衣架可以近似看成一个等腰三角形ABC,其中 , 底边BC的长 , 那么衣架的高.
11. 如图所示的衣架可以近似看成一个等腰三角形ABC,其中 , 底边BC的长 , 那么衣架的高.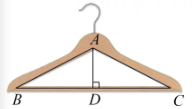 12. 如图四边形中, , 则四边形面积为.
12. 如图四边形中, , 则四边形面积为.
三、作图题
-
13. 如图所示为有16个边长为1的小正方形拼成的网格图,每个小正方形的顶点叫做格点,请按照要求画图.
 (1)、在图1中画出1个面积为3的 , 顶点C在格点上;(2)、在图2中画出2个以为腰的等腰、 , 且这两个三角形不全等,点C、D都在格点上;(3)、在图3中画出2个以为斜边的直角三角形 , , 点C、D均在各点上.
(1)、在图1中画出1个面积为3的 , 顶点C在格点上;(2)、在图2中画出2个以为腰的等腰、 , 且这两个三角形不全等,点C、D都在格点上;(3)、在图3中画出2个以为斜边的直角三角形 , , 点C、D均在各点上.四、综合题
-
14. △ABC中,AB=AC,E为AC中点,F为BE上一点,且CE=CF.若△ABC的三条边长均为偶数,且BF与BE两条线段长度的乘积为20. 求△ABC的周长.
 15. 如图,某住宅小区在施工过程中留下了一块空地,已知米,米, , 米,米,小区为美化环境,欲在空地上铺草坪.
15. 如图,某住宅小区在施工过程中留下了一块空地,已知米,米, , 米,米,小区为美化环境,欲在空地上铺草坪. (1)、是直角三角形吗?为什么?(2)、小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?
(1)、是直角三角形吗?为什么?(2)、小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?
-

