【每日15min】16 直角三角形—浙教版数学八（上）微专题复习

试卷更新日期：2023-10-22 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图所示.在△ABC中，∠C=90°，DE垂直平分AB，交BC于点E，垂足为点D，BE=6cm，∠B=15°，则AC等于（）

A、6cm B、5cm C、4cm D、3cm

查看试题解析
2. 如图，边长为a的等边△ABC中，BF是AC上中线且BF＝b，点D在BF上，连接AD，在AD的右侧作等边△ADE，连接EF，则△AEF周长的最小值是（）

A、 $\frac{1}{2} a + \frac{2}{3} b$ B、 $\frac{1}{2} a + b$ C、a+ $\frac{1}{2}$ b D、 $\frac{3}{2}$ a

查看试题解析
3. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B = 30 °$ ， D为BC上一点， $C D = A D = 4$ ，则BC的长为（）

A、10 B、12 C、14 D、16

查看试题解析
4. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ C = 30 °$ ，点 $D$ 在 $B C$ 上， $A B ⊥ A D$ ， $A D = 2$ ，则 $B C$ 的长为（）

A、4 B、5 C、6 D、8

查看试题解析
5. 如图，在等腰三角形 $A B C$ 中， $A B = A C = 4$ ， $∠ B A C = 30 °$ ， $A G$ 是底边 $B C$ 上的高，在 $A G$ 的延长线上有一个动点D，连接 $C D$ ，作 $∠ C D E = 150 °$ ，交 $A B$ 的延长线于点E， $∠ C D E$ 的角平分线交 $A B$ 边于点F，则在点D运动的过程中，线段 $E F$ 的最小值（）

A、6 B、4 C、3 D、2

查看试题解析
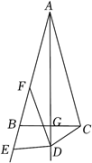6. 如图，在 $R t △ A B C$ 中， $∠ A = 90 °$ ， $B D$ 平分 $∠ A B C$ ，交 $A C$ 于点D，若点D恰好在边 $B C$ 的垂直平分线上，则∠C的度数为（）

A、30 B、36 C、40 D、45

查看试题解析
7. 如图，在 $Rt △ ABC$ 中， $∠ ACB = 90 °$ ，分别以 $A$ 点， $B$ 点为圆心以大于 $\frac{1}{2} AB$ 为半径画弧，两弧交于 $E$ ， $F$ ，连接 $EF$ 交 $AB$ 于点 $D$ ，连接 $CD$ ，以 $C$ 为圆心， $CD$ 长为半径作弧，交 $AC$ 于 $G$ 点，则 $CG$ ： $AB =$ （）

A、1： $\sqrt{5}$ B、1：2 C、1： $\sqrt{3}$ D、1： $\sqrt{2}$

查看试题解析
8. 如图，在△ABC中，∠ACB＝90°，点D是AB的中点．连接CD，若CD+AB=7.5，则CD的长度是（）

A、1.5 B、2 C、2.5 D、5

查看试题解析

二、填空题

9. 如图，∠AOP=∠BOP=15°，PC $/ /$ OA，PD⊥OA，若PC=4，则∠COP= ， PD=.

查看试题解析
10. 如图，在Rt△ABC中，∠A=90°，∠B=30°，CD平分∠ACB交AB于点D，DE∥BC，交AC于点E，若BC=9，则AE的长为．

查看试题解析
11. 将两块全等的直角三角板如图放置，其中一块三角板的斜边恰好经过另一块三角板的直角顶点 $O$ 及斜边上的中点 $A$ ，若这两块三角板的斜边长为 $13.6 c m$ ，则 $O A =$ .

查看试题解析
12. 如图，在 $Rt △ A B C$ 中，斜边 $A B$ 上的中线CD=5，则 $A B =$ ．

查看试题解析

三、作图题

13. 如图，河l同侧有一块直角三角形的绿化带 $A B C$ ， $∠ C = 90 °$ ， $∠ B = 30 °$ ， $B C = 40 m$ ， $C A ⊥ l$ .A到河l的距离等于 $C A$ 的长度.需要用水管从河l上一点P处分别引水到A ， B两处，并通过安装在这两处的喷水龙头灌溉草地.

(1)、请在河l上画出点P的位置，使得从点P向A ， B两处引水所需的水管总长度最短；

(2)、求至少需要水管多少米（连接处接头长度忽略不计）.

查看试题解析

四、解答题

14. 在△ABC中，AB＝BC＝2，∠ABC＝90°，BP是AC边上的高线，将一块三角板的直角顶点放在点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AB、BC于D、E两点．图1和图2是旋转三角板得到的图形中的两种情况．

(1)、求证：BP＝CP；

(2)、猜想线段PD与PE之间的数量关系，并结合图1证明你的结论；

(3)、在三角板绕点P旋转的整个过程中，当△PEC为等腰三角形时，求BE的长．

查看试题解析
15. 问题情境
在综合与实践课上，老师让同学们以“两条平行线AB，CD和一块含60°角的直角三角尺EFG(∠EFG=90°，∠EGF=60°)”为主题开展数学活动。

操作发现

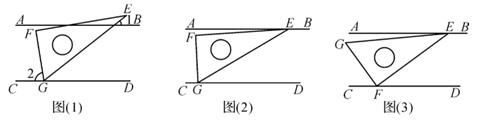
(1)、如图(1)，小明把三角尺的60°角的顶点G放在CD上，若∠2=2∠1，求∠1的度数；

(2)、如图(2)，小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上，请你探索并说明∠AEF与∠FGC之间的数量关系；

(3)、如图(3)，小亮把三角尺的直角顶点F放在CD上，30°角的顶点E落在AB上，若∠AEG=a，请直接写出∠CFG的度数(用含a的式子表示)

查看试题解析
16. 数学课上，老师在黑板上展示了如下一道探究题：
在 $△ A B C$ 中， $A B = A C = m$ ， $∠ B A C = α$ ，点D，E分别在边AC，AB上，且 $C E = B D$ ，试探究线段AE和线段AD的数量关系.

(1)、初步尝试
如图①，若 $α = 90 °$ ，请探究AE和AD的数量关系，并说明理由.

(2)、类比探究
如图②，若 $α = 120 °$ ，小组讨论后，有小组利用120°的角作垂线构造直角三角形，通过证明两次三角形全等，得到AE和AD的数量关系仍然成立，请你写出推理过程；

(3)、延伸拓展
如图③，将第（2）中的“点E在边AB上”改为“点E在边BA的延长线上”，其它条件不变，请探究AE和AD的数量关系（用含m的式子表示），并说明理由.

查看试题解析