广西南宁2023-2024学年八年级上册数学第一次月考试卷
试卷更新日期:2023-10-20 类型:月考试卷
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 如图所示的个图案中是轴对称图形的是( )A、
 阿基米德螺旋线
B、
阿基米德螺旋线
B、 笛卡尔心形线
C、
笛卡尔心形线
C、 赵爽弦图
D、
赵爽弦图
D、 太极图
2. 2023的相反数是( )A、 B、 C、 D、3. 下列长度的各组线段中,能组成三角形的是( )A、1,2,3 B、2,3,5 C、3,4,8 D、3,4,54. 如图,CM是的中线, , 则BM的长为( )
太极图
2. 2023的相反数是( )A、 B、 C、 D、3. 下列长度的各组线段中,能组成三角形的是( )A、1,2,3 B、2,3,5 C、3,4,8 D、3,4,54. 如图,CM是的中线, , 则BM的长为( )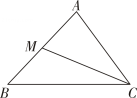 A、7cm B、6cm C、5cm D、4cm5. 若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )A、60° B、50° C、40° D、30°6. 下列各图中,正确画出AC边上的高的是( )A、
A、7cm B、6cm C、5cm D、4cm5. 若一个直角三角形其中一个锐角为40°,则该直角三角形的另一个锐角是( )A、60° B、50° C、40° D、30°6. 下列各图中,正确画出AC边上的高的是( )A、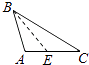 B、
B、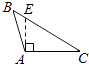 C、
C、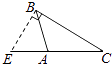 D、
D、 7. 一个多边形的内角和等于540°,则它的边数为( )A、4 B、5 C、6 D、88. 如图若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )
7. 一个多边形的内角和等于540°,则它的边数为( )A、4 B、5 C、6 D、88. 如图若△ABE≌△ACF,且AB=5,AE=2,则EC的长为( )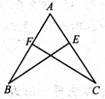 A、2 B、3 C、4 D、59. 如图,若与关于直线对称,交于点则下列说法中不一定正确的是( )
A、2 B、3 C、4 D、59. 如图,若与关于直线对称,交于点则下列说法中不一定正确的是( )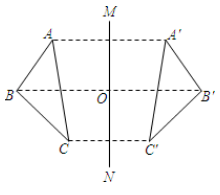 A、 B、 C、 D、10. 某地兴建的幸福小区的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,想在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该在 ( )
A、 B、 C、 D、10. 某地兴建的幸福小区的三个出口A、B、C的位置如图所示,物业公司计划在不妨碍小区规划的建设下,想在小区内修建一个电动车充电桩,以方便业主,要求到三个出口的距离都相等,则充电桩应该在 ( ) A、三条高线的交点处 B、三条中线的交点处 C、三个角的平分线的交点处 D、三条边的垂直平分线的交点处11. 若关于x的不等式组的整数解共有三个,则a的取值范围是( ).A、 B、 C、 D、12. 已知:是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、O同时在不等边的内部时,那么和的数量关系是( )
A、三条高线的交点处 B、三条中线的交点处 C、三个角的平分线的交点处 D、三条边的垂直平分线的交点处11. 若关于x的不等式组的整数解共有三个,则a的取值范围是( ).A、 B、 C、 D、12. 已知:是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、O同时在不等边的内部时,那么和的数量关系是( )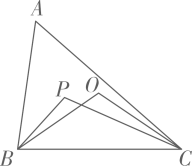 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共12.0分)
-
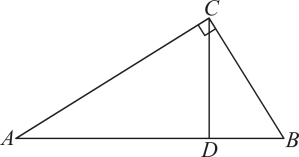
13. 计算: =14. 在平面直角坐标系中,点 关于x轴对称的点的坐标为 .15. 如图,是的高, . 若 , 则的度数是 .
 16. 如图,把一张长方形的纸片沿折叠,若 , 则的度数为.
16. 如图,把一张长方形的纸片沿折叠,若 , 则的度数为.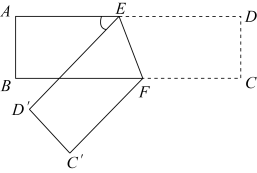 17. 如图,在中, , , , , BC的长是.
17. 如图,在中, , , , , BC的长是.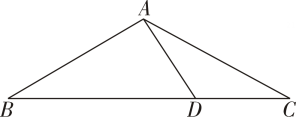 18. 如图, , 点在射线上,点在射线上,均为等边三角形,从左起第1个等边三角形的边长记为 , 第2个等边三角形的边长记为 , 以此类推,若 , 则 .
18. 如图, , 点在射线上,点在射线上,均为等边三角形,从左起第1个等边三角形的边长记为 , 第2个等边三角形的边长记为 , 以此类推,若 , 则 .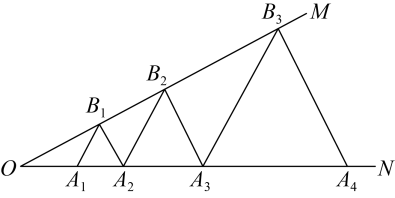
三、解答题(本大题共8小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
-
19. 计算:.20. 如图,和相交于点 , , .
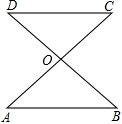
求证: .
21. 校学生处为了了解全校名学生每天在上学路上所用的时间,随机调查了名学生下面是某一天这名学生上学所用时间单位:分钟: , , , , , , , , , , , , , , , , , , , , , , , , , , , , , .通过整理和分析数据,得到如下不完全的统计图.
根据所给信息,解答下列问题:
 (1)、补全条形统计图;(2)、这名学生上学所用时间的中位数为分钟,众数为分钟;(3)、若随机问这名同学中其中一名学生的时间,最有可能得到的回答是分钟;(4)、估计全校学生上学所用时间在分钟及以下的人数.22. 如图,已知在平面直角坐标系中, 的顶点坐标分别为 , , .
(1)、补全条形统计图;(2)、这名学生上学所用时间的中位数为分钟,众数为分钟;(3)、若随机问这名同学中其中一名学生的时间,最有可能得到的回答是分钟;(4)、估计全校学生上学所用时间在分钟及以下的人数.22. 如图,已知在平面直角坐标系中, 的顶点坐标分别为 , , .
⑴请在平面直角坐标系中画出 ;
⑵画出与 关于 轴对称的 ,请直接写出点 , 的坐标;
⑶求出 的面积.
23. 阅读理解题初二(1)班同学到野外上数学活动课,为测量池塘两端、的距离,设计了如下方案:
(Ⅰ)如图 , 先在平地上取一个可直接到达、的点 , 连接、 , 并分别延长至 , 延长至 , 使 , , 最后测出的距离即为的长;
(Ⅱ)如图 , 先过点作的垂线 , 再在上取、两点使 , 接着过作的垂线 , 交的延长线于 , 则测出的长即为的距离.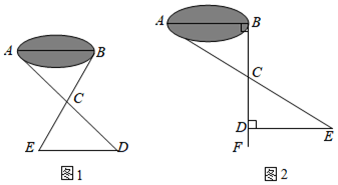
阅读后回答下列问题:
(1)、方案Ⅰ是否可行?请直接说出结论.(2)、方案Ⅱ是否可行?请说明理由.(3)、方案Ⅱ中作 , 目的是;(4)、若仅满足 , 方案Ⅱ是否成立? ▲ .24. 如图,在等边中,点D,E,F分别在边AB,BC,CA上.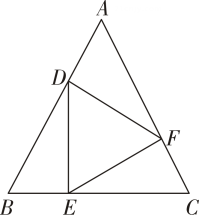 (1)、若.求证:是等边三角形;(2)、若是等边三角形,成立吗?若成立,请给予证明;若不成立,请说明理由.25. 某印刷厂每月生产甲、乙两种练习本共40万本,且所有练习本当月全部卖出,其中成本、售价如表所示.
(1)、若.求证:是等边三角形;(2)、若是等边三角形,成立吗?若成立,请给予证明;若不成立,请说明理由.25. 某印刷厂每月生产甲、乙两种练习本共40万本,且所有练习本当月全部卖出,其中成本、售价如表所示.品种
甲
乙
成本
1.2元/本
0.4元/本
售价
1.6元/本
0.6元/本
(1)、若该印刷厂五月份的利润为11万元,求生产甲、乙两种练习本分别是多少万本;(2)、某学校计划用7680元的经费到该印刷厂采购练习本.经商讨,该公司同意甲种练习本售价打九折,乙种练习本不能让利.若学校能采购到1万本,且不超支,问最多能购买甲种练习本多少本?26. 如图,在平面直角坐标系中, , , 且 .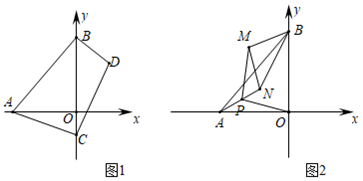 (1)、求 , 的值;(2)、如图 , 为轴负半轴上一点,连 , 过点作 , 使 , 连求证:;(3)、如图 , 若有一等腰 , , 连 , 取中点 , 连、试探究和的关系.
(1)、求 , 的值;(2)、如图 , 为轴负半轴上一点,连 , 过点作 , 使 , 连求证:;(3)、如图 , 若有一等腰 , , 连 , 取中点 , 连、试探究和的关系.