浙江省金华市义乌市五校2023-2024学年八年级上册数学第一次学情调查试卷
试卷更新日期:2023-10-20 类型:月考试卷
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知,在△ABC中,∠A=60°,∠C=80°,则∠B=( )A、60° B、30° C、20° D、40°3. 若等腰三角形的两边长分别为4和6,则它的周长是( )A、14 B、15 C、16 D、14或164. 下列命题为真命题的有( )
2. 已知,在△ABC中,∠A=60°,∠C=80°,则∠B=( )A、60° B、30° C、20° D、40°3. 若等腰三角形的两边长分别为4和6,则它的周长是( )A、14 B、15 C、16 D、14或164. 下列命题为真命题的有( )①内错角相等;②无理数都是无限小数:③在同一平面内,过一点有且只有一条直线与已知直线垂直;④过一点有且只有一条直线与已知直线平行
A、0个 B、1个 C、2个 D、3个5. 尺规作图作的平分线的方法如下:如图,以点为圆心,任意长为半径作弧,交 , 于点 , , 再分别以点 , 为圆心,以大于长为半径作弧,两弧交于点 , 作射线由作法得到的根据是.( )
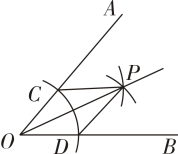 A、 B、 C、 D、6. 如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为( )
A、 B、 C、 D、6. 如图,点D在BC的延长线上,DE⊥AB于点E,交AC于点F.若∠A=35°,∠D=15°,则∠ACB的度数为( )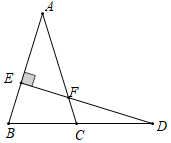 A、65° B、70° C、75° D、85°7. 如图,在△ABC中,∠C=90°,AC=8,DC= AD,BD平分∠ABC,则点D到AB的距离等于( )
A、65° B、70° C、75° D、85°7. 如图,在△ABC中,∠C=90°,AC=8,DC= AD,BD平分∠ABC,则点D到AB的距离等于( )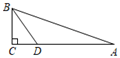 A、4 B、3 C、2 D、18. 如图, ABC是等腰三角形,点O 是底边BC上任意一点,OE、OF分别与两边垂直,等腰三角形ABC的腰长为5,面积为12,则OE+OF的值为( )
A、4 B、3 C、2 D、18. 如图, ABC是等腰三角形,点O 是底边BC上任意一点,OE、OF分别与两边垂直,等腰三角形ABC的腰长为5,面积为12,则OE+OF的值为( )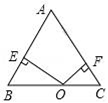 A、4 B、 C、15 D、89. 如图, , 分别平分 , , 且点到的距离 , 的周长为 , 则的面积为( )
A、4 B、 C、15 D、89. 如图, , 分别平分 , , 且点到的距离 , 的周长为 , 则的面积为( ) A、 B、 C、 D、10. 如图, , 、、分别平分的外角、内角、外角以下结论:
A、 B、 C、 D、10. 如图, , 、、分别平分的外角、内角、外角以下结论:
;;
;平分 .
其中正确的结论有( )
A、个 B、个 C、个 D、个二、填空题(本大题共6小题,共24.0分)
-
11. 写出命题“两个全等三角形的面积相等”的逆命题 .12. 如果等腰三角形的周长是27cm,一腰上的中线把三角形分成两个三角形,其周长之差 是3cm,则这个等腰三角形的底边长为cm.13. 如图,在中,已知 , , , 则度.
 14. 如图, , , 于点 , 于点若 , , 则 .
14. 如图, , , 于点 , 于点若 , , 则 .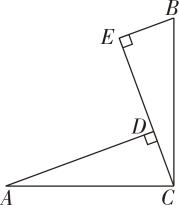 15. 如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19cm , △ABD的周长为13cm , 则AE的长为 .
15. 如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19cm , △ABD的周长为13cm , 则AE的长为 . 16. 如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为.
16. 如图,在四边形ABCD中,∠DAB=130°,∠D=∠B=90°,点M,N分别是CD,BC上两个动点,当△AMN的周长最小时,∠AMN+∠ANM的度数为.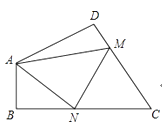
三、解答题(共8小题,17-19题6分,20-21题8分,22-23题10分,24题12分,共66分)
-
17. 如图,点和点在内部.请你作出点 , 使点到点和点的距离相等,且到两边的距离相等保留作图痕迹,不写作法;
 18. 如图,在中,是边上的高.
18. 如图,在中,是边上的高. (1)、若是边上的中线, , , 求的长;(2)、若是的平分线, , , 求的大小.19. 若 , 是的两边,且 .(1)、试求 , 的值,并求第三边的取值范围;(2)、若是等腰三角形,试求此三角形的周长.20. 如图,点、、、在一条直线上, , , 求证:
(1)、若是边上的中线, , , 求的长;(2)、若是的平分线, , , 求的大小.19. 若 , 是的两边,且 .(1)、试求 , 的值,并求第三边的取值范围;(2)、若是等腰三角形,试求此三角形的周长.20. 如图,点、、、在一条直线上, , , 求证: (1)、≌;(2)、 .21. 如图,在中, , 为边上的高,平分 , 分别交 , 于点 , , 求证: .
(1)、≌;(2)、 .21. 如图,在中, , 为边上的高,平分 , 分别交 , 于点 , , 求证: . 22. 如图,在中,是角平分线, , 分别为 , 上的点,且与有何数量关系请说明理由.
22. 如图,在中,是角平分线, , 分别为 , 上的点,且与有何数量关系请说明理由. 23. 已知:是直线上的一点,射线是的角平分线, .
23. 已知:是直线上的一点,射线是的角平分线, . (1)、如图,当是锐角时,求证: .(2)、探究:当是直角或钝角时,中的结论“”还成立吗?说明理由.24. 小明在学习过程中,对教材中的一个有趣问题做如下探究:
(1)、如图,当是锐角时,求证: .(2)、探究:当是直角或钝角时,中的结论“”还成立吗?说明理由.24. 小明在学习过程中,对教材中的一个有趣问题做如下探究: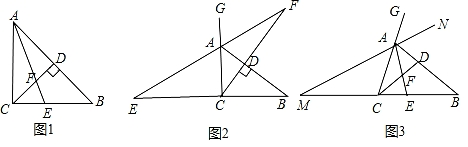
【习题回顾】已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
【变式思考】如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
【探究延伸】如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.