湖北省广水市2023-2024学年九年级上学期数学第一阶段考试试卷
试卷更新日期:2023-10-20 类型:月考试卷
一、选择题(每小题3分,共30分)
-
1. 用配方法解方程 , 原方程变形为( )A、 B、 C、 D、2. 下列垃圾分类标识的图案中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 二次函数图像向左平移1个单位长度,得到的二次函数解析式为( )A、 B、 C、 D、4. 关于的方程有实数根,则满足( )A、 B、 , 且 C、且 D、5. 已知二次函数 , 当时,随的增大而减小,则有( )A、 B、 C、 D、6. 一个三角形的两边长分列为3和6,第三边长是方程的根,则这个三角形的周长是( )A、11 B、11或13 C、13 D、都不对7. 在同一平面直角坐标系中,一次函数 和二次函数 的图象大致为( )A、
3. 二次函数图像向左平移1个单位长度,得到的二次函数解析式为( )A、 B、 C、 D、4. 关于的方程有实数根,则满足( )A、 B、 , 且 C、且 D、5. 已知二次函数 , 当时,随的增大而减小,则有( )A、 B、 C、 D、6. 一个三角形的两边长分列为3和6,第三边长是方程的根,则这个三角形的周长是( )A、11 B、11或13 C、13 D、都不对7. 在同一平面直角坐标系中,一次函数 和二次函数 的图象大致为( )A、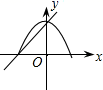 B、
B、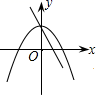 C、
C、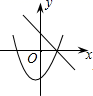 D、
D、 8. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的种植面积为600平方米,则小道的宽为多少米?若设小道的宽为米,则根据题意,列方程为( )
8. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的种植面积为600平方米,则小道的宽为多少米?若设小道的宽为米,则根据题意,列方程为( ) A、 B、 C、 D、9. 如图,正方形四个顶点的坐标依次为.若抛物线y=ax2与正方形有公共点,则实数a的取值范围是( )
A、 B、 C、 D、9. 如图,正方形四个顶点的坐标依次为.若抛物线y=ax2与正方形有公共点,则实数a的取值范围是( ) A、 B、 C、 D、10. 如图是二次函数的图像一部分,是对称轴,有下列判断:①;②;③;④若是抛物线上两点,则 , 其中正确的是( )
A、 B、 C、 D、10. 如图是二次函数的图像一部分,是对称轴,有下列判断:①;②;③;④若是抛物线上两点,则 , 其中正确的是( ) A、①②③ B、①③④ C、①②④ D、②③④
A、①②③ B、①③④ C、①②④ D、②③④二、填空题(每小题3分,共18分)
-
11. 二次函数 的最大值是 .12. 若m,n是方程的两个实数根,则的值为.13. 某药品原价每盆25元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒16元,则该药品平均每次降价的百分率是.14. 对于实数p,q,我们用符号表示p,q两数中较小的数,如min.若, , 则值为.15. 如图,在中, , 将绕点顺时针旋转得到 , 点C的对应点落在BC边上,且B' , 则的度数为.
 16. 如图,在平面直角坐标系中,点在找物线上,过点作轴的垂线,交抛物线于另一点B,点C、D在线段AB上,且C、D两点关于轴对称,过点C作轴的垂线交抛物线于点.连接 , 当是等腰三角形时,线段CD的长为.
16. 如图,在平面直角坐标系中,点在找物线上,过点作轴的垂线,交抛物线于另一点B,点C、D在线段AB上,且C、D两点关于轴对称,过点C作轴的垂线交抛物线于点.连接 , 当是等腰三角形时,线段CD的长为.
三、解答题(共9小题,合计72分)
-
17. 解下列方程:(1)、(2)、18. 如图,在等腰三角形ABC中, , 是上一点,将AE绕点A逆时针旋转得到AD,连接DE,CD.
 (1)、求证△ABE≌△ACD;(2)、当BC=6,CE=2时,求DE的长.19. 已知关于x的一元二次方程有实数根.(1)、求的取值范围:(2)、如果该方程的两个实数根为 , 且 , 求的取值范围.20. 如图,有长为30m的篱笆,一面利用墙(墙的最大可用度度为10m),围成中间隔有一道篱笆(平行于的长方形花圃.
(1)、求证△ABE≌△ACD;(2)、当BC=6,CE=2时,求DE的长.19. 已知关于x的一元二次方程有实数根.(1)、求的取值范围:(2)、如果该方程的两个实数根为 , 且 , 求的取值范围.20. 如图,有长为30m的篱笆,一面利用墙(墙的最大可用度度为10m),围成中间隔有一道篱笆(平行于的长方形花圃. (1)、设花园的一边AB为xm,则BC的长可用含的代数式表示为m.(2)、当AB的长度是多少米时,围成的花圃面积为3平方米?21. 阅读下面材料,然后解答问题:
(1)、设花园的一边AB为xm,则BC的长可用含的代数式表示为m.(2)、当AB的长度是多少米时,围成的花圃面积为3平方米?21. 阅读下面材料,然后解答问题:解方程:(x2-6)3-(x2-6)-2=0.
分析:本题实际上为一元四次方程,若展开按常规方法解答,对同学们来说具有一定的挑战性.解高次方程的基本方法是“降次”,我们发现本方程是以为基本结构搭建的,所以我们可以把视为一个整体,设为另外一个未知数,就可以把原方程降次为一元二改方程来继续解答.我们把这种换元解方程的方法叫做换元法.
解:设 , 则原方程换元为.
或
解得
或
解得:
请参考例题解法,解下列方程:
(1)、;(2)、.22. 国庆假期一部《长津湖》带给我们极大的震撼,面对美军的先进武器,志愿军不怕牺牲,以一敌百,更是有很多技术精湛的“神投手”.某志愿军身负重伤,不轻易放弃,用最后一丝力气投出一枚手榴弹,如果把该志愿军投出的手榴弹轨迹作为一抛物线,如图所示,手榴弹的最大高度为10米,此时水平飞行距离为9米,手榴弹离手点离地面高度为1.9米. (1)、求此抛物线解析式;(2)、求志愿军同志的手榴弹扔了多远?23. 某商场销售一款小商品,进货价为40元/件.当销售单价为60元时,每天的销售量为300件.在销售过程中发现:销售单价每上涨2元,每天的销售量就减少20件.设销售单价上涨x元(x为偶数),每天的销售量为y件.(1)、求y与x之间的函数关系式;(2)、设每天的销售利润为w元,为了减少库存,则该商品的销售单价定为多少元时,每天获得的利润最大?最大利润是多少?24. 某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(单位:件)与每件售价x(单位:元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天销售量为95件.(1)、求y与x之间的函数关系式:(2)、若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?(3)、设该商店销售这种消毒用品每天获得w元,当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?25. 如图,抛物线与轴交于两点,过点的直线交抛物线于点.
(1)、求此抛物线解析式;(2)、求志愿军同志的手榴弹扔了多远?23. 某商场销售一款小商品,进货价为40元/件.当销售单价为60元时,每天的销售量为300件.在销售过程中发现:销售单价每上涨2元,每天的销售量就减少20件.设销售单价上涨x元(x为偶数),每天的销售量为y件.(1)、求y与x之间的函数关系式;(2)、设每天的销售利润为w元,为了减少库存,则该商品的销售单价定为多少元时,每天获得的利润最大?最大利润是多少?24. 某商店购进了一种消毒用品,进价为每件8元,在销售过程中发现,每天的销售量y(单位:件)与每件售价x(单位:元)之间存在一次函数关系(其中8≤x≤15,且x为整数).当每件消毒用品售价为9元时,每天的销售量为105件;当每件消毒用品售价为11元时,每天销售量为95件.(1)、求y与x之间的函数关系式:(2)、若该商店销售这种消毒用品每天获得425元的利润,则每件消毒用品的售价为多少元?(3)、设该商店销售这种消毒用品每天获得w元,当每件消毒用品的售价为多少元时,每天的销售利润最大?最大利润是多少元?25. 如图,抛物线与轴交于两点,过点的直线交抛物线于点. (1)、求抛物线的解析式;(2)、P是线段AC上的一个动点(点P不与端点A,C重合),过点P作x轴的垂线交抛物线于点E,求线段PE最大时点P的坐标;(3)、F是抛物线上的动点,在x轴上是否存在点D,使得以点A,C,D,F为顶点的四边形是平行四边形?如果存在,请求出所有满足条件的点D的坐标;如果不存在,请说明理由.
(1)、求抛物线的解析式;(2)、P是线段AC上的一个动点(点P不与端点A,C重合),过点P作x轴的垂线交抛物线于点E,求线段PE最大时点P的坐标;(3)、F是抛物线上的动点,在x轴上是否存在点D,使得以点A,C,D,F为顶点的四边形是平行四边形?如果存在,请求出所有满足条件的点D的坐标;如果不存在,请说明理由.