广西壮族自治区钦州市2023-2024学年八年级上册数学9月月考试卷
试卷更新日期:2023-10-20 类型:月考试卷
一、选择题(本大题共12小题,共60分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列每组数分别表示三根木棒的长,将它们首尾连接后,能摆成三角形的一组是( )A、1,2,3 B、1,2,4 C、2,3,4 D、2,2,42. 已知为的中线,且 , , 则与的周长之差为( )A、 B、 C、 D、3. 已知三角形的两边长分别为 和 ,第三边长为整数,则该三角形的周长为( )A、 B、 C、 D、4. 满足下列条件的△ABC中,不是直角三角形的是( )A、∠A=2∠B=3∠C B、∠B+∠A=∠C C、两个内角互余 D、∠A:∠B:∠C=2:3:55. 如图,点D、E分别在线段BC、AC上,连接AD、BE.若∠A=35°,∠B=25°,∠C=50°,则∠1的大小为( )
 A、60° B、70° C、75° D、85°6. 在下列条件中: , :::: , , , 中,能确定是直角三角形的条件有
A、60° B、70° C、75° D、85°6. 在下列条件中: , :::: , , , 中,能确定是直角三角形的条件有( )
A、个 B、个 C、个 D、个7. 如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠BAC=60°,∠ABE=25°,则∠DAC的大小是( )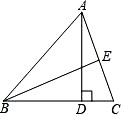 A、15° B、20° C、25° D、30°8. 如图,在中, , , , 则( )
A、15° B、20° C、25° D、30°8. 如图,在中, , , , 则( ) A、 B、 C、 D、9. 在△ABC中,∠A= ∠B= ∠C,则此三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形10. 如图, , 垂足为点 , , , 则的度数为( )
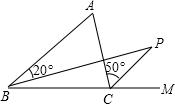
A、 B、 C、 D、9. 在△ABC中,∠A= ∠B= ∠C,则此三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形10. 如图, , 垂足为点 , , , 则的度数为( ) A、 B、 C、 D、11. 小明把一副含 , 的直角三角板如图摆放,其中 , , , 则等于( )
A、 B、 C、 D、11. 小明把一副含 , 的直角三角板如图摆放,其中 , , , 则等于( ) A、 B、 C、 D、12. 如图,中, , 沿将此三角形对折,又沿再一次对折,点落在上的处,此时 , 则原三角形的的度数为
A、 B、 C、 D、12. 如图,中, , 沿将此三角形对折,又沿再一次对折,点落在上的处,此时 , 则原三角形的的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共4小题,共20分)
-
13. 如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠P=°.
 14. 在中, , , 点在边上,连接 , 若为直角三角形,则的度数为 .15. 我们定义三边长均为整数的三角形叫做整三角形.已知是整三角形,其周长为偶数,若则边长的最小值是 .16. 如图,在中, , , 于点 , 于点 , 与交于点 , 则 .
14. 在中, , , 点在边上,连接 , 若为直角三角形,则的度数为 .15. 我们定义三边长均为整数的三角形叫做整三角形.已知是整三角形,其周长为偶数,若则边长的最小值是 .16. 如图,在中, , , 于点 , 于点 , 与交于点 , 则 .
三、解答题(本大题共4小题,共40分。解答应写出文字说明,证明过程或演算步骤)