湖北省黄冈市2023-2024学年八年级上册数学月考试卷
试卷更新日期:2023-10-20 类型:月考试卷
一、选择题(每空3分,共27分)
-
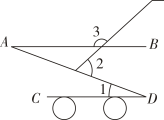
1. 下列实数中,最大的数是( )A、0 B、 C、 D、42. 的值等于( )A、 B、0.03 C、0.3 D、3. 如图是一款手推车的平面示意图,其中 , , , 则为( )
 A、66° B、56° C、98° D、104°4. 下列调查中,调查方式选择合理的是( )A、为了了解全国中学生的视力情况,选择全面调查 B、为了了解一批袋装食品是否含有防腐剂,选择全面调查 C、为了检测某城市的空气质量,选择抽样调查 D、为了检测乘坐飞机的旅客是否携带违禁物品,选择抽样调查5. 若点在第二象限,则点在哪个象限( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 《算法统宗》是明代数学家程大位所著的一部实用数学著作,也是明代数学的代表作.书中有一首类似二元一次方程组的饮酒数学诗:“肆中饮客醉颜生,试问高明能算士,几多醨酒几多醇?”这首诗是说,好酒二瓶,可以醉倒5位客人;薄酒三瓶,可以醉倒二位客人,如果34位客人醉倒了,他们总共饮下16瓶酒.试问:其中好酒、薄酒分别是多少瓶?设有好酒x瓶,薄酒y瓶.依题意,可列方程组为( )A、 B、 C、 D、7. 下列各选项中能用“垂线段最短”来解释的现象是( )A、
A、66° B、56° C、98° D、104°4. 下列调查中,调查方式选择合理的是( )A、为了了解全国中学生的视力情况,选择全面调查 B、为了了解一批袋装食品是否含有防腐剂,选择全面调查 C、为了检测某城市的空气质量,选择抽样调查 D、为了检测乘坐飞机的旅客是否携带违禁物品,选择抽样调查5. 若点在第二象限,则点在哪个象限( )A、第一象限 B、第二象限 C、第三象限 D、第四象限6. 《算法统宗》是明代数学家程大位所著的一部实用数学著作,也是明代数学的代表作.书中有一首类似二元一次方程组的饮酒数学诗:“肆中饮客醉颜生,试问高明能算士,几多醨酒几多醇?”这首诗是说,好酒二瓶,可以醉倒5位客人;薄酒三瓶,可以醉倒二位客人,如果34位客人醉倒了,他们总共饮下16瓶酒.试问:其中好酒、薄酒分别是多少瓶?设有好酒x瓶,薄酒y瓶.依题意,可列方程组为( )A、 B、 C、 D、7. 下列各选项中能用“垂线段最短”来解释的现象是( )A、 测量跳远成绩
B、
测量跳远成绩
B、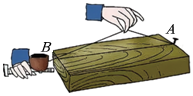 木板上弹墨线
C、
木板上弹墨线
C、 两钉子固定木条
D、
两钉子固定木条
D、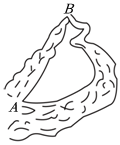 弯曲河道改直
8. 关于x的不等式的所有整数解和的为0,则m的取值范围是( )A、 B、 C、 D、
弯曲河道改直
8. 关于x的不等式的所有整数解和的为0,则m的取值范围是( )A、 B、 C、 D、二、填空题(每小题3分,共24分)
-
9. 若 是关于 的一元一次不等式,则 的值为。10. 若是方程的一个解,则的值为.11. 设n为正整数,且 , 则n的值为.12. 如图,直线AB与直线CD相交于点O,OE平分 , 若 , 且 , 则.
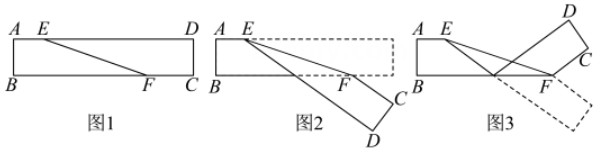
 13. 在平面直角坐标系中, , , 若轴, , 则.14. 某文具店一款笔记本的进价为每本6元,售价为每本9元.该店老板“6.18”准备对这款笔记本打折销售,为使得利润率不低于5%,该笔记本最多可以打折.15. 如图1是长方形纸带, , 将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中度数是.
13. 在平面直角坐标系中, , , 若轴, , 则.14. 某文具店一款笔记本的进价为每本6元,售价为每本9元.该店老板“6.18”准备对这款笔记本打折销售,为使得利润率不低于5%,该笔记本最多可以打折.15. 如图1是长方形纸带, , 将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中度数是.
 16. 如图,点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……,按这样的运动规律,经过第2025次运动后动点P的坐标是 .
16. 如图,点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……,按这样的运动规律,经过第2025次运动后动点P的坐标是 .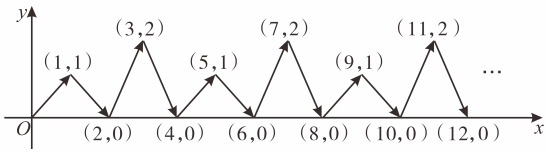
三、解答题(共72分)
-
17. 计算: .18. 某校想了解学生每周课外阅读的时间情况,随机调查了部分学生,对学生每周课外阅读时间x小时进行分组整理,并绘制了不完整的频数分面直方图和扇形统计图(如图),根据图中提供的信息,解答下列问题:
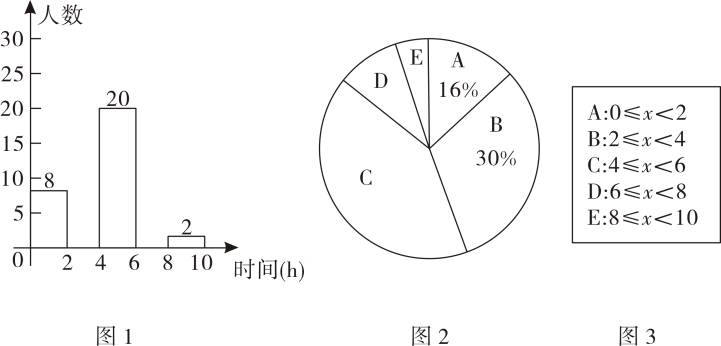 (1)、这次抽样调查的学生人数是人;(2)、扇形统计图中“B”组对应的圆心角为°;(3)、请将频数分布直方图补充完整,并在图标出数据;(4)、若该校共有2000名学生,试估计全校有多少名学生每周课外阅读时间不少于6小时?19.(1)、已知的算术平方根是4,的立方根是3,求的值.(2)、已知a是的整数部分,b是它的小数部分,求的值.20. 如图所示,已知 , 现将向上平移4个单位长度,再向左平移2个单位长度,得到 , 其中A',B',C'分别为点A,B,C的对应点.
(1)、这次抽样调查的学生人数是人;(2)、扇形统计图中“B”组对应的圆心角为°;(3)、请将频数分布直方图补充完整,并在图标出数据;(4)、若该校共有2000名学生,试估计全校有多少名学生每周课外阅读时间不少于6小时?19.(1)、已知的算术平方根是4,的立方根是3,求的值.(2)、已知a是的整数部分,b是它的小数部分,求的值.20. 如图所示,已知 , 现将向上平移4个单位长度,再向左平移2个单位长度,得到 , 其中A',B',C'分别为点A,B,C的对应点.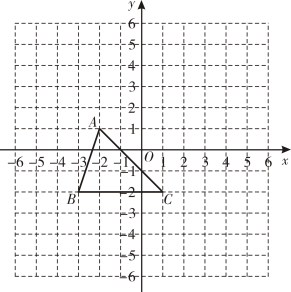 (1)、请在网格中画出 , 并直接写出的坐标C'( ▲ , ▲ );(2)、已知AB边上一点P经过上述平移后的对应点为 , 请直接写出点P坐标( , );(3)、一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,也可以通过原来的图形作一次平移得到,求线段BC在一次平移过程中扫过的面积.21. 如图,已知 , .
(1)、请在网格中画出 , 并直接写出的坐标C'( ▲ , ▲ );(2)、已知AB边上一点P经过上述平移后的对应点为 , 请直接写出点P坐标( , );(3)、一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,也可以通过原来的图形作一次平移得到,求线段BC在一次平移过程中扫过的面积.21. 如图,已知 , .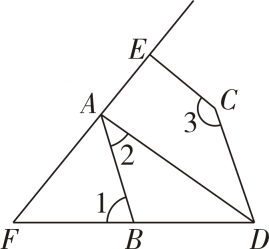 (1)、判断AC与DE的位置关系,并说明理由;(2)、若CA平分 , 于点E, , 求的度数.22. 已知关于x,y的二元一次方程组.(1)、若 , 求a的值;(2)、若 , 求a的取值范围;(3)、在(2)的条件下,化简.23. 某商店决定购进A、B两种小礼品.若购进A种小礼品15件,B种小礼品10件,需要450元;A种小礼品9件,B种小礼品12件,需360元.(1)、求A、B两种小礼品每件进价各多少元?(2)、若该商店决定购进这两种小礼品共100件,考虑市场需求和资金周围,用于购买这100件小礼品的资金不少于1800元,但不超过1812元,那么该商店共有哪几种进货方案?(3)、已知该商店出售一件A种小礼品可获利t元,出售一件B种小礼品可获利元,在(2)的条件下,商店采用哪种进货方案获利最多?(商店出售的小礼品标价均不低于进价)24. 如图,在平面直角坐标中,点 , 满足.
(1)、判断AC与DE的位置关系,并说明理由;(2)、若CA平分 , 于点E, , 求的度数.22. 已知关于x,y的二元一次方程组.(1)、若 , 求a的值;(2)、若 , 求a的取值范围;(3)、在(2)的条件下,化简.23. 某商店决定购进A、B两种小礼品.若购进A种小礼品15件,B种小礼品10件,需要450元;A种小礼品9件,B种小礼品12件,需360元.(1)、求A、B两种小礼品每件进价各多少元?(2)、若该商店决定购进这两种小礼品共100件,考虑市场需求和资金周围,用于购买这100件小礼品的资金不少于1800元,但不超过1812元,那么该商店共有哪几种进货方案?(3)、已知该商店出售一件A种小礼品可获利t元,出售一件B种小礼品可获利元,在(2)的条件下,商店采用哪种进货方案获利最多?(商店出售的小礼品标价均不低于进价)24. 如图,在平面直角坐标中,点 , 满足.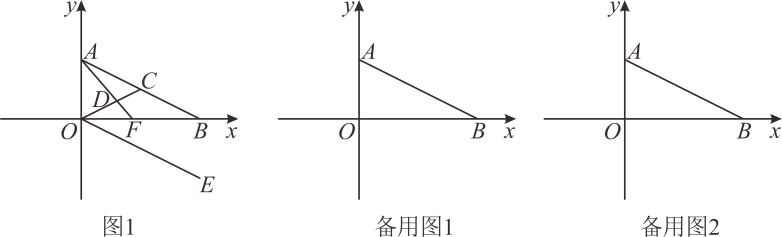 (1)、直接写出结果:点A坐标为 , 点B坐标为;(2)、点C是线段AB上一点,满足 , 点E是第四象限中一点,连接OE,使得 , 点F是线段上一动点,连接AF交OC于点D,当点F在线段上运动时,是否为定值?如果是,请求出该值;如果不是,请说明理由;(3)、已知坐标轴上有两动点P、Q同时出发,P点从A点出发以每秒1个单位长度的速度向下匀速移动,Q点从O点出发以每秒2个单位长度的速度向右匀速移动,点是线段AB上一点,设运动时间为秒,当时,
(1)、直接写出结果:点A坐标为 , 点B坐标为;(2)、点C是线段AB上一点,满足 , 点E是第四象限中一点,连接OE,使得 , 点F是线段上一动点,连接AF交OC于点D,当点F在线段上运动时,是否为定值?如果是,请求出该值;如果不是,请说明理由;(3)、已知坐标轴上有两动点P、Q同时出发,P点从A点出发以每秒1个单位长度的速度向下匀速移动,Q点从O点出发以每秒2个单位长度的速度向右匀速移动,点是线段AB上一点,设运动时间为秒,当时,①求此时t的值;
②此时是否存在点 , 使得 , 若存在,请直接写出H的坐标;若不存在,请说明理由.