福建省福州四十中2023-2024学年八年级上册数学第一次适应性考试试卷
试卷更新日期:2023-10-20 类型:月考试卷
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下列各组数可能是一个三角形的边长的是( )A、 , , B、 , , C、 , , D、 , ,2. 若的三个内角之比为:: , 则一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形3. 若一个多边形的内角和为1080°,则这个多边形的边数为()
A、6 B、7 C、8 D、94. 如图, , 相交于点 , , 要根据“”证明≌ , 还需添加的一个条件是( ) A、 B、 C、 D、5. 如图,≌ , 图中和相等的线段( )
A、 B、 C、 D、5. 如图,≌ , 图中和相等的线段( ) A、线段 B、线段 C、线段 D、线段6. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A、线段 B、线段 C、线段 D、线段6. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )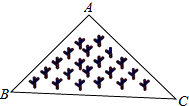 A、△ABC的三条中线的交点 B、△ABC三条角平分线的交点 C、△ABC三条高所在直线的交点 D、△ABC三边的中垂线的交点7. 如图,在中, , 以为圆心,任意长为半径画弧,分别交、于点 , , 再以、为圆心,大于的长为半径作弧,两弧交于点 , 作射线交于点 , 若 , , 则( )
A、△ABC的三条中线的交点 B、△ABC三条角平分线的交点 C、△ABC三条高所在直线的交点 D、△ABC三边的中垂线的交点7. 如图,在中, , 以为圆心,任意长为半径画弧,分别交、于点 , , 再以、为圆心,大于的长为半径作弧,两弧交于点 , 作射线交于点 , 若 , , 则( ) A、 B、 C、 D、8. 如图,在中,是高和的交点,且 , 已知 , , 则长为( )
A、 B、 C、 D、8. 如图,在中,是高和的交点,且 , 已知 , , 则长为( ) A、 B、 C、 D、9. 如图,是等腰直角三角形, , 已知点的坐标为 , 点的坐标为 , 则点的坐标为( )
A、 B、 C、 D、9. 如图,是等腰直角三角形, , 已知点的坐标为 , 点的坐标为 , 则点的坐标为( ) A、 B、 C、 D、10. 如图,在中, , , 点为的中点,则的长可能是( )
A、 B、 C、 D、10. 如图,在中, , , 点为的中点,则的长可能是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共7小题,共21.0分)
-
11. 已知直角三角形的一个锐角为 , 则它的另一个锐角的度数为 .12. 如图,已知△ABC≌△ADE,若AB=7,AC=3,则BE的值为
 13. 已知:如图,的两个外角的平分线交于点 , 如果 , 则 .
13. 已知:如图,的两个外角的平分线交于点 , 如果 , 则 .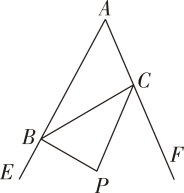 14. 如图,≌ , 若 , , 则等于 .
14. 如图,≌ , 若 , , 则等于 . 15. 如图,小亮从点出发,沿直线前进米后向左转 , 再沿直线前进米,又向左转 , , 照这样走下去,他第一次回到出发地点时,一共走了米.
15. 如图,小亮从点出发,沿直线前进米后向左转 , 再沿直线前进米,又向左转 , , 照这样走下去,他第一次回到出发地点时,一共走了米. 16. 将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5=
16. 将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5=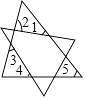 17. 如图,射线AB与射线CD平行,点F为射线AB上的一定点,连接CF,点P是射线CD上的一个动点(不包括端点C),将 沿PF折叠,使点C落在点E处.若 ,当点E到点A的距离最大时, .
17. 如图,射线AB与射线CD平行,点F为射线AB上的一定点,连接CF,点P是射线CD上的一个动点(不包括端点C),将 沿PF折叠,使点C落在点E处.若 ,当点E到点A的距离最大时, .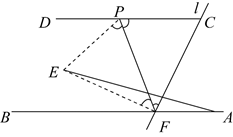
三、解答题(本大题共9小题,共89.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 如图,、分别是的高和角平分线, , , 求的度数.
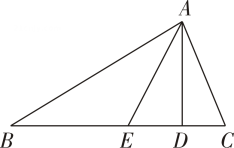 19. 若一个多边形内角和与外角和的比为:求这个多边形的边数.20. 如图,、是线段上两点,且 , , , 求证: .
19. 若一个多边形内角和与外角和的比为:求这个多边形的边数.20. 如图,、是线段上两点,且 , , , 求证: . 21. 如图,在△ABC中,∠A=∠DBC=36°,∠C=72°.求∠1,∠2的度数.
21. 如图,在△ABC中,∠A=∠DBC=36°,∠C=72°.求∠1,∠2的度数. 22. 如图,已知 .
22. 如图,已知 . (1)、用直尺和圆规按下列要求作图,保留作图痕迹:在上作点 , 使点到和的距离相等.(2)、过点作交的延长线于点 , 作 , 垂足为求证: .23. 如图, , , . , 与 交于点 .
(1)、用直尺和圆规按下列要求作图,保留作图痕迹:在上作点 , 使点到和的距离相等.(2)、过点作交的延长线于点 , 作 , 垂足为求证: .23. 如图, , , . , 与 交于点 .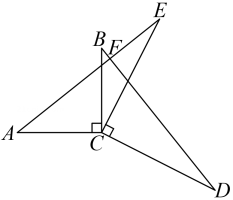 (1)、求证: ;(2)、求 的度数.24. 如图,在中,平分 , 且平分 , 垂足为 , 于点 , 于点 .
(1)、求证: ;(2)、求 的度数.24. 如图,在中,平分 , 且平分 , 垂足为 , 于点 , 于点 . (1)、求证:;(2)、若 , , 求的长.
(1)、求证:;(2)、若 , , 求的长.

