福建省福州十九中2023-2024学年八年级上册数学开门考试卷
试卷更新日期:2023-10-20 类型:开学考试
一、选择题(本大题共10小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列实数中,无理数是( )A、 B、 C、 D、3. 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
2. 下列实数中,无理数是( )A、 B、 C、 D、3. 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( ) A、60° B、65° C、75° D、85°4. 下列说法正确的是( )A、从全校名学生中抽取名调查了解寒假阅读情况,抽取的样本容量为 B、了解北京冬奥会的收视率适合用抽样调查 C、调查某批次汽车的抗撞击能力适合用全面调查 D、旅客乘坐飞机前的安检适合用抽样调查5. 如图,将三角形沿着方向平移得到三角形 , 则下列结论错误的是( )
A、60° B、65° C、75° D、85°4. 下列说法正确的是( )A、从全校名学生中抽取名调查了解寒假阅读情况,抽取的样本容量为 B、了解北京冬奥会的收视率适合用抽样调查 C、调查某批次汽车的抗撞击能力适合用全面调查 D、旅客乘坐飞机前的安检适合用抽样调查5. 如图,将三角形沿着方向平移得到三角形 , 则下列结论错误的是( )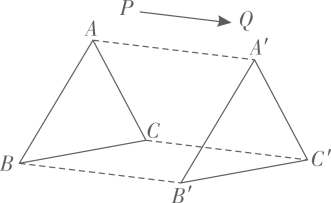 A、 . B、 C、 D、6. 如果 , 则下列结论中正确的是( )A、 B、 C、 D、7. 如果一个多边形的内角和与外角和相等,那么这个多边形的边数是( )A、 B、 C、 D、8. 能说明命题“对于任何实数 , ”,是假命题的一个反例可以是( )A、 B、 C、 D、9. 我国古代数学著作九章算术卷七“盈不足”中有这样一个问题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”意思是:几个人合伙买一件物品,每人出元,则余元;若每人出元,则少元,问几人合买?这件物品多少钱?若设有人合买,这件物品元,则根据题意列出的二元一次方程组为( )A、 B、 C、 D、10. 如图, , 点是的中点,平分 , 且 , 则点到线段的最小距离为( )
A、 . B、 C、 D、6. 如果 , 则下列结论中正确的是( )A、 B、 C、 D、7. 如果一个多边形的内角和与外角和相等,那么这个多边形的边数是( )A、 B、 C、 D、8. 能说明命题“对于任何实数 , ”,是假命题的一个反例可以是( )A、 B、 C、 D、9. 我国古代数学著作九章算术卷七“盈不足”中有这样一个问题:“今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?”意思是:几个人合伙买一件物品,每人出元,则余元;若每人出元,则少元,问几人合买?这件物品多少钱?若设有人合买,这件物品元,则根据题意列出的二元一次方程组为( )A、 B、 C、 D、10. 如图, , 点是的中点,平分 , 且 , 则点到线段的最小距离为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共24.0分)
-
11. 9的算术平方根是 .12. 如图,是的中线, , , 那么的周长比的周长多 .
 13. 若点在轴上,则 .14. 如图,已知 , , , 且 , 则点的坐标是 .
13. 若点在轴上,则 .14. 如图,已知 , , , 且 , 则点的坐标是 .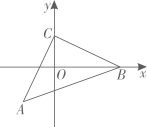 15. 已知实数 , , , 满足 , 若 , 则的最大值为 .16. 如图,在中, , 角平分线、交于点 , 于点下列结论:
15. 已知实数 , , , 满足 , 若 , 则的最大值为 .16. 如图,在中, , 角平分线、交于点 , 于点下列结论:
::;
;
;
,
其中正确结论是 .
三、计算题(本大题共1小题,共8.0分)
-
17.(1)、解二元一次方程组 .(2)、若上述方程组的解是关于 , 的二元一次方程的一组解,求代数式的值.
四、解答题(本大题共8小题,共78.0分。解答应写出文字说明,证明过程或演算步骤)
-
18. 计算: .19. 解不等式: , 并将解集在数轴上表示出来.20. 如图, , , 点、在线段上,且 , 连接、 .
求证: .
 21. 如图,在中, .
21. 如图,在中, . (1)、尺规作图,在上求作一点 , 使不要求写作法,保留作图痕迹;请你根据所学的三角形全等的有关知识,作图依据是 提示:、、、(2)、若(1)中 , , 求的度数.22. 某校组织名学生参加“展示我美丽祖国”庆国庆的自拍照片的评比活动,随机取一些学生在评比中的成绩制成的统计图表如下:
(1)、尺规作图,在上求作一点 , 使不要求写作法,保留作图痕迹;请你根据所学的三角形全等的有关知识,作图依据是 提示:、、、(2)、若(1)中 , , 求的度数.22. 某校组织名学生参加“展示我美丽祖国”庆国庆的自拍照片的评比活动,随机取一些学生在评比中的成绩制成的统计图表如下:频数分布表
分数段
频数
百分比
根据以上图表提供的信息,解答下列问题:
(1)、该调查的样本容量是 .(2)、 , , ;补全频数分布直方图;(3)、如果评比成绩在分及以上含分的可以获奖,试估计该校参加此次活动获奖的人数.23. “绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:村庄
清理养鱼网箱人数/人
清理捕鱼网箱人数/人
总支出/元
A
15
9
57000
B
10
16
68000
(1)、若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;(2)、在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?24.(一)阅读材料
若关于 , 的二元一次方程有一组整数解 , 则方程的全体整数解可表示为为整数 .
例题:求关于 , 的二元一次方程的所有正整数解.
小明参考阅读材料,解决该例题如下:
解: , ,
, 要取整数,当时, ,
该方程一组整数解为 , 其全体整数解为为整数 .
, .
为整数,、或 .
该方程的正整数解为、和 .
(二)解决问题
(1)、关于 , 的二元一次方程的全体整数解表示为(t为整数),则;(2)、请参考阅读材料,直接写出关于 , 的二元一次方程的一组整数解和它对应的全体整数解;(3)、请你参考小明的解题方法,求关于 , 的二元一次方程的全体正整数解.25. 已知:平面直角坐标系中,如图 , 点 , 轴于点 , 并且满足 . (1)、试判断的形状并说明理由.(2)、如图 , 若点为线段的中点,连并作 , 且 , 连交轴于点 , 试求点的坐标.(3)、如图 , 若点为点的左边轴负半轴上一动点,以为一边作交轴负半轴于点 , 连 , 在点运动过程中,试猜想式子的值是否发生变化?若不变,求这个不变的值;若发生变化,试求它变化的范围.
(1)、试判断的形状并说明理由.(2)、如图 , 若点为线段的中点,连并作 , 且 , 连交轴于点 , 试求点的坐标.(3)、如图 , 若点为点的左边轴负半轴上一动点,以为一边作交轴负半轴于点 , 连 , 在点运动过程中,试猜想式子的值是否发生变化?若不变,求这个不变的值;若发生变化,试求它变化的范围.
-